Multimediální knihovna Pyglet: podpora pro tvorbu modelů kvadrik, disků a kruhových výsečí přes GLU

V knihovně Pyglet neexistuje žádná přímá podpora pro vykreslení složitějších těles, nabízeno je „pouze“ rozhraní ke knihovnám OpenGL a GLU. Ale právě existence rozhraní pro knihovnu GLU (OpenGL Utility Library) nám umožní do trojrozměrných scén přidat základní 3D tělesa (koule, válce, kužely), pomocné 2D tvary (disky, mezikruží a kruhové výseče) a v případě potřeby i NURB (Non-uniform rational B-spline) plochy.

Obsah

1. Podpora pro tvorbu modelů kvadrik, disků a kruhových výsečí v knihovně GLU

2. Co značí pojem „kvadrika“?

3. Postup pro vytvoření a zobrazení kvadrik při použití GLU

4. Vytvoření trojrozměrného modelu koule

5. První demonstrační příklad: vykreslení modelu koule

6. Vytvoření modelu válce nebo kužele

7. Druhý demonstrační příklad: vykreslení modelu válce

8. Třetí demonstrační příklad: vykreslení modelu kužele

9. Vytvoření disku či mezikruží

10. Čtvrtý demonstrační příklad: vykreslení mezikruží

11. Vytvoření kruhové výseče

12. Pátý demonstrační příklad: vykreslení kruhové výseče

13. Změna parametrů vykreslovaných kvadrik

14. Šestý demonstrační příklad: vykreslení koule s interaktivní změnou všech parametrů modelu

15. Repositář s demonstračními příklady

16. Funkce knihovny GLU popsané v tomto článku

17. Odkazy na Internetu

1. Podpora pro tvorbu modelů kvadrik, disků a kruhových výsečí v knihovně GLU

Důležitá úvodní poznámka: v moderním OpenGL se setkáme s jiným přístupem k vykreslování trojrozměrných těles, v němž se používá programovatelná vykreslovací pipeline a unifikovaný formát vstupních dat, což mimo jiné znamená, že se již nepoužívají příkazy glBegin() a glEnd() (tento režim se nazývá immediate mode). I přesto může být knihovna GLU užitečná, neboť nám umožní vykreslit základní 3D tvary velmi jednoduše, prakticky jen třemi příkazy. Se současným způsobem práce s vykreslovací pipeline (zejména s použitím VBO – Vertex Buffer Objects), který je rychlejší a flexibilnější, se setkáme ve třinácté a čtrnácté části tohoto seriálu.

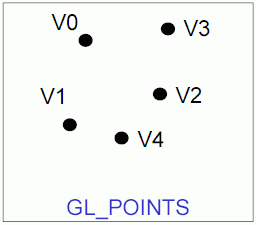
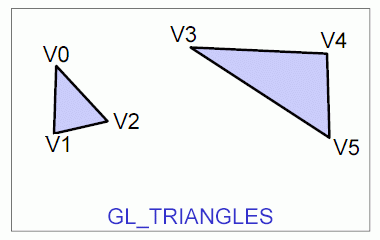
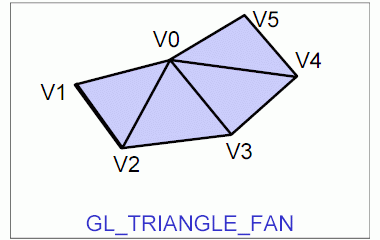
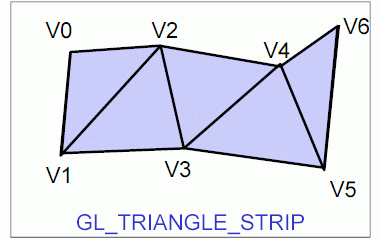
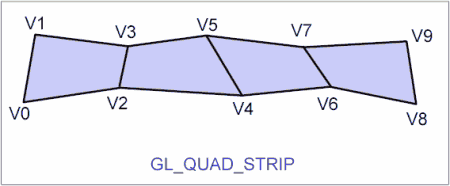
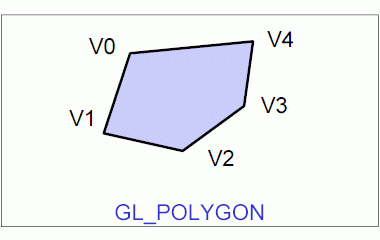
Knihovna OpenGL nabízí programátorům podporu pro vykreslování pouze základních grafických primitiv, z nichž se skládají složitější objekty. Mezi tato primitiva patří body, úsečky, polyčáry (na sebe navazující úsečky), trojúhelníky, pruhy trojúhelníků, trsy trojúhelníků, čtyřúhelníky a pruhy čtyřúhelníků. Poněkud složitější geometrické tvary jsou podporovány až knihovnou GLU, která je ovšem z Pygletu taktéž dostupná. Jedná se v první řadě o takzvané kvadriky. Mezi základní podporované kvadriky patří tělesa ve tvaru koule, válce a kužele. Taktéž je možné pracovat s plošným tělesem ve tvaru disku a kruhového výřezu. Složitější kvadriky, mezi něž patří různé hyperboloidy, paraboloidy, sedlové plochy atd., je možné vytvořit buď s využitím programově spočítané trojúhelníkové sítě nebo NURBS ploch, kterými se v tomto seriálu budeme v dalších částech taktéž zabývat.

Obrázek 1: Grafické primitivum GL_POINTS.

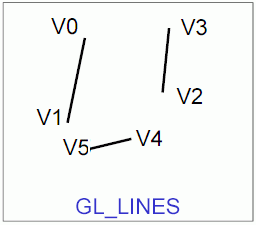
Obrázek 2: Grafické primitivum GL_LINES.

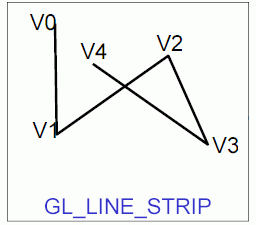
Obrázek 3: Grafické primitivum GL_LINE_STRIP.

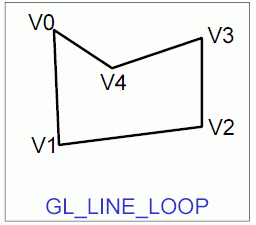
Obrázek 4: Grafické primitivum GL_LINE_LOOP.

Obrázek 5: Grafické primitivum GL_TRIANGLES.

Obrázek 6: Grafické primitivum GL_TRIANGLE_FAN.

Obrázek 7: Grafické primitivum GL_TRIANGLE_STRIP.

Obrázek 8: Grafické primitivum GL_QUADS.

Obrázek 9: Grafické primitivum GL_QUAD_STRIP.

Obrázek 10: Grafické primitivum GL_POLYGON.

2. Co značí pojem „kvadrika“?

Před popisem funkcí nabízených knihovnou, které umožňují práci s kvadrikami, si nejdříve řekněme, co to vlastně kvadrika je. Pojmem kvadrika se v matematice a přeneseně i v počítačové grafice označují trojrozměrná tělesa, jejichž povrch (plocha) je určena implicitní funkcí:

f(x, y, z)=0

kde implicitní funkce f(x, y, z) nabývá tvaru:

f(x, y, z) = a₁x² + a₂y² + a₃z² + a₄xy + a₅yz + a₆xz + a₇x + a₈y + a₉z + a₁₀

(jinými slovy - jedná se, podle nejvyšší použité mocniny, o algebraické plochy druhého stupně).

To mj. znamená, že pro zadané parametry implicitní plochy a₁-a₁₀ je možné zjistit, zda bod P=[x, y, z] leží či neleží na ploše kvadriky. Podle znaménka výsledku funkce f(x, y, z) lze dokonce zjistit, zda bod leží uvnitř či vně kvadriky – to samozřejmě platí pouze pro uzavřené plochy, nikoli plochy nekonečné, jako je hyperboloid. Pro některé hodnoty parametrů je výše zmíněná rovnice v oboru reálných čísel neřešitelná (tj. neexistují takové hodnoty x, y, z pro které by funkce f nabývala nuly), proto takovou kvadriku nelze sestrojit.

Obrázek 11: Některé vybrané kvadriky vykreslené raytracerem PovRay.

Mezi nejznámější a nejpoužívanější kvadriky v matematice patří:

Elipsoid:
x²/a²+y²/b²+z²/c²-1=0 (uvádím nejpoužívanější tvar rovnice, převod na výše zmíněný formát je triviální).
Hyperboloid:
x²/a²+y²/b²-z²/c²=+-1.
Paraboloid:
x²/p+-y²/q=2z.

Speciálním případem elipsoidu je koule, válec lze získat dosazením vhodných hodnot do implicitní rovnice hyperboloidu. Takto získaný válec je nekonečný, tj. neobsahuje obě „víčka“, ale pouze plášť.

Kvadriky se často používají v některých CAD a CAM aplikacích, kde se z nich (a případně i z dalších tvarů – roviny, poloprostoru a toroidu) vytváří složitější tělesa s využitím konstruktivní geometrie těles (Constructive Solid Geometry, CSG). Většina programů pro fotorealistické zobrazování scén pomocí raytracingu také CSG (a tím pádem i kvadriky, alespoň ty základní) využívá. Z této kategorie programů je pro Linux i další platformy dostupný především volně šiřitelný raytracer POVRay.

Pokud se vrátíme zpět ke knihovnám GLU a OpenGL, je nutné říct, že GLU neumožňuje vytvářet všechny možné kvadriky, ale pouze ty nejzákladnější: koule a válce (resp. kužele, válce jsou v pojetí GLU speciálním případem kuželů). K tomu lze vytvářet i disky (plošné těleso) a jejich výřezy, což se hodí zejména pro uzavírání různých „děr“ ve vznikajícím modelu tělesa.

3. Postup pro vytvoření a zobrazení kvadrik při použití GLU

Pro vytvoření a následné vykreslení kvadrik ve vznikající trojrozměrné scéně je nutné dodržet následující postup:

vytvořit nový objekt pro následné renderování kvadrik pomocí funkce gluNewQuadric().
nastavit atributy pro rendering (vykreslování) tohoto objektu, v některých případech je však možné ponechat původní nastavení. Změna atributů kvadrik se provádí s využitím funkcí gluQuadricDrawStyle(), gluQuadricOrientation(), gluQuadricNormals() a gluQuadricTexture().
zaregistrovat callback funkci, která je volaná v případě výskytu chyby při renderování kvadriky. Registrace callback funkce se provede zavoláním funkce gluQuadricCallback() (není vyložené nutné).
zavolat funkci pro vytvoření požadované kvadriky: gluSphere(), gluCylinder(), gluDisk() nebo gluPartialDisk().
po vykreslení požadované kvadriky je možné objekt pro renderování kvadrik smazat (tj. odstranit z paměti jeho atributy) pomocí funkce gluDeleteQuadric().

Poznámka: při práci s kvadrikami se ve všech funkcích pracuje s referencí na objekt typu GLUquadric. V dokumentaci ke knihovně GLU se sice stále mluví o objektu (má některé objektové vlastnosti, kromě polymorfismu a dědičnosti), ve skutečnosti ale jde o běžnou C-čkovou datovou strukturu. Ostatně celá knihovna GLU je postavena na čistém jazyce C, což zjednodušuje volání jejich funkcí i z programů vytvořených v jiných programovacích jazycích. A právě této vlastnosti využijeme v demonstračních příkladech, které jsou psané v programovacím jazyku Python – budeme pracovat s céčkovským ukazatelem přes ctypes.

4. Vytvoření trojrozměrného modelu koule

Koule, jež patří mezi nejjednodušší kvadriky (pokud vynecháme lineární struktury, které jsou podmnožinou kvadrik), je popsána rovnicí:

x²+y²+z²-r²=0,

kde r značí poloměr koule.

Z předchozí rovnice plyne, že jediným parametrem, kterým je takto definovaná koule specifikována, je právě poloměr r. Střed koule leží v počátku souřadného systému, což však nepředstavuje při práci s modelem významnější problém, jelikož je možné souřadný systém natáčet a posouvat změnou transformačních matic, tj. pomocí funkcí glTranslatef() a glRotatef().

Funkce pro vytvoření modelu koule pomocí kvadrik se jmenuje gluSphere() a má v Pythonu následující deklaraci:

def gluSphere(
    quadric,
    radius,
    slices,
    stacks
)

Význam jednotlivých parametrů této funkce:

V prvním parametru quadric se předává ukazatel na dříve vytvořený objekt kvadriky.
Ve druhém parametru radius se předává hodnota značící poloměr vytvářené koule. Ve skutečnosti se jedná o nadbytečný údaj, protože se velikost koule dá změnit i pomocí úpravy transformačních matic, zde však nedochází ke změně měřítka normálových vektorů.
Ve třetím parametru slices se předává počet „poledníků“ pomocí nichž je koule rozdělena na jednotlivé plošky. Čím je tento údaj větší, tím více ploškami bude koule tvořena a tím přesnější bude její model (sníží se samozřejmě rychlost vykreslování).
Ve čtvrtém parametru stacks se předává počet „rovnoběžek“ pomocí nichž je koule rozdělena na plošky. Počet rovnoběžek je o jedničku nižší než zde zadaná hodnota. To znamená, že pokud je do parametru stacks zapsána hodnota 2, vytvoří se pouze jedna rovnoběžka – rovník a dva póly, mezi kterými jsou vytvořeny vykreslované plošky.

Obrázek 12: Model koule vykreslený prvním příkladem.

5. První demonstrační příklad: vykreslení modelu koule

V dnešním prvním demonstračním příkladu je vykreslen model koule, a to konkrétně ve funkci draw_quadric
. V této funkci se nejdříve nastaví vlastnosti vykreslování, konkrétně fakt, že se má koule vykreslit jako drátový model. Následně se specifikuje výpočet normálových vektorů a koule je vykreslena příkazem gluSphere(). Následně je objekt reprezentující kvadriku odstraněn:

def draw_quadric():
    radius = 8.0
    slices = 10
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    gluSphere(quadric, radius, slices, stacks)  # vykresleni kvadriky
    gluDeleteQuadric(quadric)                   # zruseni kvadriky

Obrázek 13: Model koule vykreslený prvním příkladem.

Samotné vykreslení je realizováno ve funkci on_draw(), v níž se současně reaguje na stisk kurzorových kláves sloužících pro otáčení koulí ve scéně:

@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers()
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_quadric()                         # vykresleni dratoveho modelu koule

Úplný zdrojový kód prvního demonstračního příkladu vypadá následovně:

#!/usr/bin/env python

import pyglet
from pyglet.gl import *
from pyglet.window import key

fov = 70.0                                 # zorny uhel (field of view)
nearPlane = 0.1                            # blizsi orezavaci rovina
farPlane = 90.0                            # vzdalenejsi orezavaci rovina

r1 = 0.0
r2 = 0.0


window = pyglet.window.Window(width=500,
                              height=500,
                              caption="Pyglet library")

keys = key.KeyStateHandler()
window.push_handlers(keys)


def init():
    glClearColor(0.0, 0.0, 0.3, 0.0)       # barva pozadi obrazku
    glPolygonMode(GL_FRONT, GL_FILL)       # nastaveni rezimu vykresleni modelu
    glPolygonMode(GL_BACK, GL_FILL)

    # zakaz odstranovani hran nebo sten podle jejich normal
    glDisable(GL_CULL_FACE)

    glShadeModel(GL_SMOOTH)                # nastaveni stinovaciho rezimu


@window.event
def on_resize(width, height):
    init()
    glViewport(0, 0, width, height)        # viditelna oblast pres cele okno


def draw_quadric():
    radius = 8.0
    slices = 10
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    gluSphere(quadric, radius, slices, stacks)  # vykresleni kvadriky
    gluDeleteQuadric(quadric)                   # zruseni kvadriky


def clear_buffers():
    # vymazani vsech bitovych rovin barvoveho bufferu
    glClear(GL_COLOR_BUFFER_BIT)


def set_projection_matrix(fov, nearPlane, farPlane):
    # zacatek modifikace projekcni matice
    glMatrixMode(GL_PROJECTION)
    # vymazani projekcni matice (=identita)
    glLoadIdentity()
    gluPerspective(fov, 1.0, nearPlane, farPlane)


def set_modelview_matrix(rotation1, rotation2):
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()                       # nahrat jednotkovou matici

    gluLookAt(4.0, 6.0, 18.0,              # bod, odkud se kamera diva
              0.0, 2.0,  0.0,              # bod, kam se kamera diva
              0.0, 1.0,  0.0)              # poloha "stropu" ve scene

    glRotatef(rotation1, 1.0, 0.0, 0.0)    # rotace objektu
    glRotatef(rotation2, 0.0, 1.0, 0.0)


@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers()
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_quadric()                         # vykresleni dratoveho modelu koule


pyglet.app.run()

6. Vytvoření modelu válce nebo kužele

Mezi další kvadriky, které je možné s využitím funkcí z knihovny GLU vytvořit, patří válec a kužel. Pro oba tvary je použita stejná funkce, které se jmenuje gluCylinder() a má v Pythonu následující deklaraci:

gluCylinder(
    quadric,
    baseRadius,
    topRadius,
    height,
    slices,
    stacks
)

Význam jednotlivých parametrů této funkce je následující:

Přes první parametr quadric je předán ukazatel na dříve vytvořený objekt kvadriky, který má stejný význam jako u výše uvedené funkce gluSphere().
Ve druhém parametru baseRadius je uveden poloměr válce/kužele u jeho základny. Tato hodnota by neměla být záporná.
Ve třetím parametru topRadius je uveden poloměr válce/kužele u jeho horní základny (vrchlíku). Pokud jsou hodnoty parametrů baseRadius a topRadius shodné, vytvoří se válec, pokus jsou rozdílné, vytvoří se komolý kužel. V případě, že je parametr topRadius nastaven na nulu, vytvoří se normální kužel s jedním vrcholem.
Čtvrtým parametrem height je specifikována výška válce či kužele. Základna modelu je umístěna v počátku a osa vytvořeného tělesa směřuje vzhůru ve směru osy z. Aby byl model vycentrovaný, je zapotřebí před jeho vykreslením provést posun v záporném směru z-ové osy: glTranslatef(0.0f, 0.0f, -height/2).
V pátém parametru slices se předává počet „poledníků“, tj. dělení kolmých na základnu, pomocí nichž je válec či kužel rozdělen na jednotlivé plošky. Čím je tento údaj větší, tím více ploškami bude těleso tvořeno a tím přesnější bude jeho model (sníží se samozřejmě rychlost vykreslování).
V posledním, šestém parametru stacks se předává počet „rovnoběžek“, tj. dělení rovnoběžných se základnou, pomocí nichž je válec či kužel rozdělen na plošky. Počet rovnoběžek je o jedničku nižší než zde zadaná hodnota. To znamená, že pokud je do parametru stacks zapsána hodnota 2, vytvoří se pouze jedna rovnoběžka – „rovník“ a dvě základny o poloměrech baseRadius a topRadius, mezi kterými jsou vytvořeny vykreslované plošky.

7. Druhý demonstrační příklad: vykreslení modelu válce

Druhý příklad se do značné míry podobá příkladu prvnímu, pouze se změnil obsah funkce pro vykreslení kvadriky. Nový tvar této funkce používá volání gluCylinder() a nikoli gluSphere(). Navíc ještě celý válec posuneme ve směru Z-ové osy o hodnotu -výška_válce/2, aby došlo k jeho vycentrování na počátek světových souřadnic. Tím dosáhneme toho, že se válec bude otáčet okolo svého středu a nikoli okolo středu své podstavy:

def draw_quadric():
    baseRadius = 8.0
    topRadius = 8.0
    height = 10.0
    slices = 50
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    glTranslatef(0, 0, -height/2)               # vycentrovani valce
    gluCylinder(quadric, baseRadius, topRadius, height, slices, stacks)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky

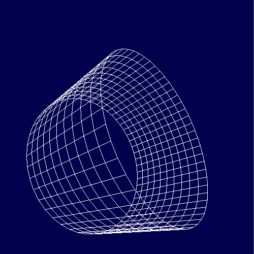
Obrázek 14: Model válce vykreslený druhým příkladem.

Následuje výpis zdrojového kódu tohoto příkladu:

#!/usr/bin/env python

import pyglet
from pyglet.gl import *
from pyglet.window import key

fov = 70.0                                 # zorny uhel (field of view)
nearPlane = 0.1                            # blizsi orezavaci rovina
farPlane = 90.0                            # vzdalenejsi orezavaci rovina

r1 = 0.0
r2 = 0.0


window = pyglet.window.Window(width=500,
                              height=500,
                              caption="Pyglet library")

keys = key.KeyStateHandler()
window.push_handlers(keys)


def init():
    glClearColor(0.0, 0.0, 0.3, 0.0)       # barva pozadi obrazku
    glPolygonMode(GL_FRONT, GL_FILL)       # nastaveni rezimu vykresleni modelu
    glPolygonMode(GL_BACK, GL_FILL)

    # zakaz odstranovani hran nebo sten podle jejich normal
    glDisable(GL_CULL_FACE)

    glShadeModel(GL_SMOOTH)                # nastaveni stinovaciho rezimu


@window.event
def on_resize(width, height):
    init()
    glViewport(0, 0, width, height)        # viditelna oblast pres cele okno


def draw_quadric():
    baseRadius = 8.0
    topRadius = 8.0
    height = 10.0
    slices = 50
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    glTranslatef(0, 0, -height/2)               # vycentrovani valce
    gluCylinder(quadric, baseRadius, topRadius, height, slices, stacks)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky


def clear_buffers():
    # vymazani vsech bitovych rovin barvoveho bufferu
    glClear(GL_COLOR_BUFFER_BIT)


def set_projection_matrix(fov, nearPlane, farPlane):
    # zacatek modifikace projekcni matice
    glMatrixMode(GL_PROJECTION)
    # vymazani projekcni matice (=identita)
    glLoadIdentity()
    gluPerspective(fov, 1.0, nearPlane, farPlane)


def set_modelview_matrix(rotation1, rotation2):
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()                       # nahrat jednotkovou matici

    gluLookAt(4.0, 6.0, 18.0,              # bod, odkud se kamera diva
              0.0, 2.0,  0.0,              # bod, kam se kamera diva
              0.0, 1.0,  0.0)              # poloha "stropu" ve scene

    glRotatef(rotation1, 1.0, 0.0, 0.0)    # rotace objektu
    glRotatef(rotation2, 0.0, 1.0, 0.0)


@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers()
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_quadric()                         # vykresleni dratoveho modelu valce


pyglet.app.run()

8. Třetí demonstrační příklad: vykreslení modelu kužele

Nepatrnou změnou jediné proměnné ve funkci:

def draw_quadric():
    baseRadius = 8.0
    topRadius = 8.0
    height = 10.0
    slices = 50
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    glTranslatef(0, 0, -height/2)               # vycentrovani valce
    gluCylinder(quadric, baseRadius, topRadius, height, slices, stacks)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky

za:

def draw_quadric():
    baseRadius = 6.0
    topRadius = 0.0
    height = 10.0
    slices = 50
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    glTranslatef(0, 0, -height/2)               # vycentrovani valce
    gluCylinder(quadric, baseRadius, topRadius, height, slices, stacks)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky

dosáhneme vykreslení kužele a nikoli válce.

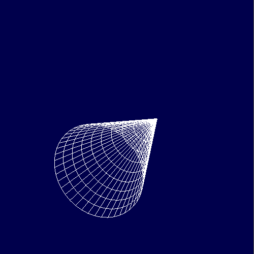
Obrázek 15: Model kužele vykreslený třetím příkladem.

Opět následuje výpis zdrojového kódu tohoto příkladu:

#!/usr/bin/env python

import pyglet
from pyglet.gl import *
from pyglet.window import key

fov = 70.0                                 # zorny uhel (field of view)
nearPlane = 0.1                            # blizsi orezavaci rovina
farPlane = 90.0                            # vzdalenejsi orezavaci rovina

r1 = 0.0
r2 = 0.0


window = pyglet.window.Window(width=500,
                              height=500,
                              caption="Pyglet library")

keys = key.KeyStateHandler()
window.push_handlers(keys)


def init():
    glClearColor(0.0, 0.0, 0.3, 0.0)       # barva pozadi obrazku
    glPolygonMode(GL_FRONT, GL_FILL)       # nastaveni rezimu vykresleni modelu
    glPolygonMode(GL_BACK, GL_FILL)

    # zakaz odstranovani hran nebo sten podle jejich normal
    glDisable(GL_CULL_FACE)

    glShadeModel(GL_SMOOTH)                # nastaveni stinovaciho rezimu


@window.event
def on_resize(width, height):
    init()
    glViewport(0, 0, width, height)        # viditelna oblast pres cele okno


def draw_quadric():
    baseRadius = 6.0
    topRadius = 0.0
    height = 10.0
    slices = 50
    stacks = 10
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    glTranslatef(0, 0, -height/2)               # vycentrovani valce
    gluCylinder(quadric, baseRadius, topRadius, height, slices, stacks)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky


def clear_buffers():
    # vymazani vsech bitovych rovin barvoveho bufferu
    glClear(GL_COLOR_BUFFER_BIT)


def set_projection_matrix(fov, nearPlane, farPlane):
    # zacatek modifikace projekcni matice
    glMatrixMode(GL_PROJECTION)
    # vymazani projekcni matice (=identita)
    glLoadIdentity()
    gluPerspective(fov, 1.0, nearPlane, farPlane)


def set_modelview_matrix(rotation1, rotation2):
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()                       # nahrat jednotkovou matici

    gluLookAt(4.0, 6.0, 18.0,              # bod, odkud se kamera diva
              0.0, 2.0,  0.0,              # bod, kam se kamera diva
              0.0, 1.0,  0.0)              # poloha "stropu" ve scene

    glRotatef(rotation1, 1.0, 0.0, 0.0)    # rotace objektu
    glRotatef(rotation2, 0.0, 1.0, 0.0)


@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers()
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_quadric()                         # vykresleni dratoveho modelu valce


pyglet.app.run()

Obrázek 16: Model kužele vykreslený třetím příkladem.

9. Vytvoření disku či mezikruží

Kromě prostorových modelů těles lze pomocí kvadrik vytvořit i plošný disk (kruh či mezikruží). Ten je možné použít například při vyplňování děr ve vytvářeném modelu, nebo pro uzavírání válců a kuželů. Vzhledem k tomu, že pomocí OpenGL není možné vykreslit kruh přímo jako grafickou primitivu (i když by analytické řešení průsečíku jednotlivých skenovacích řádků bylo jednodušší než u trojúhelníku), je model kruhu nejdříve rozdělen na několik plošek a teprve tyto jsou poslány do grafického vykreslovacího řetězce.

Počet plošek, na které je kruh rozdělen, je možné programově měnit již při jeho vytváření.

Funkce pro vytvoření disku/kruhu se jmenuje gluDisk() a má v Pythonu následující deklaraci:

gluDisk(
    quadric,
    innerRadius,
    outerRadius,
    slices,
    loops
)

Význam jednotlivých parametrů této funkce je následující:

V prvním parametru quadric funkce gluDisk() se předává ukazatel na dříve vytvořený objekt kvadriky. Význam tohoto parametru je tedy stejný jako u funkcí gluSphere() a gluCylinder().
Ve druhém parametru innerRadius je předán vnitřní poloměr disku. Pokud je vnitřní poloměr nulový, bude disk celý vyplněn a vytvoří se tak kruh. Poloměr sice může být nulový, ale neměl by být záporný.
Ve třetím parametru outerRadius je specifikován vnější poloměr disku, který by měl být větší než vnitřní poloměr. Pokud se vnitřní a vnější poloměry liší pouze o malou hodnotu (a přitom platí outerRadius>innerRadius), je výsledkem tenký prstenec.
Dalším parametrem slices je možné zadat počet řezů, tj. počet vrcholů, které jsou vytvořeny na jednotlivých prstencích.
Posledním parametrem loops se specifikuje počet prstenců, na kterých se vrcholy vytváří. Celkový počet vrcholů, ze kterých je vytvořena plocha prstence je roven hodnotě slices*loop. Podobně jako u dalších objektů reprezentovaných svou hranicí platí, že čím větší je počet vrcholů na ploše, tím přesněji je plocha vykreslena (resp. tím přesněji odpovídá matematické ploše). Na druhou stranu se samozřejmě zvyšuje zatížení sběrnice a grafického akcelerátoru, který musí zpracovat větší množství dat.

10. Čtvrtý demonstrační příklad: vykreslení mezikruží

Ve čtvrtém příkladu je vykresleno mezikruží s vnitřním poloměrem dvou délkových jednotek a vnějším poloměrem osm délkových jednotek. Pro ilustraci způsobu vytvoření tohoto tělesa se opět používá vykreslení s využitím úseček, výsledkem je tedy drátový model (wireframe):

def draw_disk():
    innerRadius = 2.0
    outerRadius = 8.0
    slices = 24
    loops = 8
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluDisk(quadric, innerRadius, outerRadius, slices, loops)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky

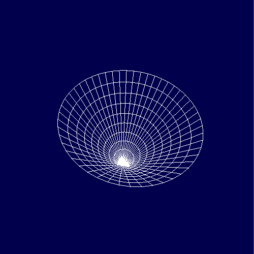
Obrázek 17: Mezikruží vykreslené čtvrtým příkladem.

Opět následuje výpis zdrojového kódu tohoto příkladu:

#!/usr/bin/env python

import pyglet
from pyglet.gl import *
from pyglet.window import key

fov = 70.0                                 # zorny uhel (field of view)
nearPlane = 0.1                            # blizsi orezavaci rovina
farPlane = 90.0                            # vzdalenejsi orezavaci rovina

r1 = 0.0
r2 = 0.0


window = pyglet.window.Window(width=500,
                              height=500,
                              caption="Pyglet library")

keys = key.KeyStateHandler()
window.push_handlers(keys)


def init():
    glClearColor(0.0, 0.0, 0.3, 0.0)       # barva pozadi obrazku
    glPolygonMode(GL_FRONT, GL_FILL)       # nastaveni rezimu vykresleni modelu
    glPolygonMode(GL_BACK, GL_FILL)

    # zakaz odstranovani hran nebo sten podle jejich normal
    glDisable(GL_CULL_FACE)

    glShadeModel(GL_SMOOTH)                # nastaveni stinovaciho rezimu


@window.event
def on_resize(width, height):
    init()
    glViewport(0, 0, width, height)        # viditelna oblast pres cele okno


def draw_disk():
    innerRadius = 2.0
    outerRadius = 8.0
    slices = 24
    loops = 8
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluDisk(quadric, innerRadius, outerRadius, slices, loops)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky


def clear_buffers():
    # vymazani vsech bitovych rovin barvoveho bufferu
    glClear(GL_COLOR_BUFFER_BIT)


def set_projection_matrix(fov, nearPlane, farPlane):
    # zacatek modifikace projekcni matice
    glMatrixMode(GL_PROJECTION)
    # vymazani projekcni matice (=identita)
    glLoadIdentity()
    gluPerspective(fov, 1.0, nearPlane, farPlane)


def set_modelview_matrix(rotation1, rotation2):
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()                       # nahrat jednotkovou matici

    gluLookAt(4.0, 6.0, 18.0,              # bod, odkud se kamera diva
              0.0, 2.0,  0.0,              # bod, kam se kamera diva
              0.0, 1.0,  0.0)              # poloha "stropu" ve scene

    glRotatef(rotation1, 1.0, 0.0, 0.0)    # rotace objektu
    glRotatef(rotation2, 0.0, 1.0, 0.0)


@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers()
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_disk()                            # vykresleni dratoveho modelu disku


pyglet.app.run()

11. Vytvoření kruhové výseče

Kruhová výseč je, podobně jako disk, rovinný útvar, který je tvořený pomocí čtyřúhelníků. Stejně jako u disků, i u kruhové výseče je nutné specifikovat vnitřní a vnější poloměr a způsob rozdělení tvaru na plošky. K těmto údajům je nutné navíc specifikovat i dva úhly, pomocí nichž se zadává tvar výseče, tj. část kruhu či prstence, která má být zobrazena.

Funkce pro vytvoření kruhové výseče se jmenuje gluPartialDisk() a má v Pythonu následující deklaraci:

gluPartialDisk(
    quadric,
    innerRadius,
    outerRadius,
    slices,
    loops,
    startAngle,
    sweepAngle
)

Význam jednotlivých parametrů této funkce je následující:

Přes první parametr quadric je předán ukazatel na dříve vytvořený model kvadriky.
Pomocí druhého parametru innerRadius je specifikován vnitřní poloměr výseče.
Pomocí třetího parametru outerRadius je specifikován vnější poloměr výseče. Pro oba poloměry platí stejné zákonitosti jako u výše popsané funkce gluDisk().
Čtvrtým parametrem slices se zadává počet řezů disku, ze kterého se výseč tvoří.
Počet prstenců, které tvoří kruhovou výseč, se předává v pátém parametru loops.
V předposledním parametru startAngle je předán první úhel kruhové výseče, který je zadán ve stupních. Hodnota tohoto úhlu může být kladná i záporná, přičemž se berou do úvahy hodnoty vypočtené „modulo“ 360.
V posledním parametru sweepAngle je předán obloukový úhel kruhové výseče, který je taktéž zadán ve stupních. Smysluplné hodnoty leží v rozsahu -360..360 stupňů, zadaná hodnota je do tohoto rozsahu ořezána.

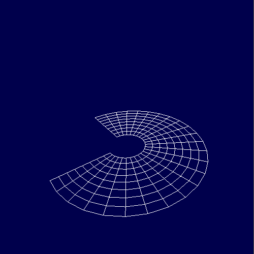
Obrázek 18: Kruhová výseč vykreslená pátým příkladem.

12. Pátý demonstrační příklad: vykreslení kruhové výseče

V dnešním předposledním demonstračním příkladu je ukázán způsob vykreslení kruhové výseče. Tento příklad je prakticky totožný s příkladem předchozím, pouze došlo ke změně funkce gluDisk() za volání funkce gluPartialDisk(). Zdrojový kód tohoto příkladu vypadá následovně:

#!/usr/bin/env python

import pyglet
from pyglet.gl import *
from pyglet.window import key

fov = 70.0                                 # zorny uhel (field of view)
nearPlane = 0.1                            # blizsi orezavaci rovina
farPlane = 90.0                            # vzdalenejsi orezavaci rovina

r1 = 0.0
r2 = 0.0


window = pyglet.window.Window(width=500,
                              height=500,
                              caption="Pyglet library")

keys = key.KeyStateHandler()
window.push_handlers(keys)


def init():
    glClearColor(0.0, 0.0, 0.3, 0.0)       # barva pozadi obrazku
    glPolygonMode(GL_FRONT, GL_FILL)       # nastaveni rezimu vykresleni modelu
    glPolygonMode(GL_BACK, GL_FILL)

    # zakaz odstranovani hran nebo sten podle jejich normal
    glDisable(GL_CULL_FACE)

    glShadeModel(GL_SMOOTH)                # nastaveni stinovaciho rezimu


@window.event
def on_resize(width, height):
    init()
    glViewport(0, 0, width, height)        # viditelna oblast pres cele okno


def draw_partial_disk():
    innerRadius = 2.0
    outerRadius = 8.0
    slices = 24
    loops = 8
    startAngle = -45
    sweepAngle = 270
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, GLU_LINE)      # nastaveni vlastnosti kvadriky
    gluPartialDisk(quadric, innerRadius, outerRadius, slices, loops,
                   startAngle, sweepAngle)
    gluDeleteQuadric(quadric)                   # zruseni kvadriky


def clear_buffers():
    # vymazani vsech bitovych rovin barvoveho bufferu
    glClear(GL_COLOR_BUFFER_BIT)


def set_projection_matrix(fov, nearPlane, farPlane):
    # zacatek modifikace projekcni matice
    glMatrixMode(GL_PROJECTION)
    # vymazani projekcni matice (=identita)
    glLoadIdentity()
    gluPerspective(fov, 1.0, nearPlane, farPlane)


def set_modelview_matrix(rotation1, rotation2):
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()                       # nahrat jednotkovou matici

    gluLookAt(4.0, 6.0, 18.0,              # bod, odkud se kamera diva
              0.0, 2.0,  0.0,              # bod, kam se kamera diva
              0.0, 1.0,  0.0)              # poloha "stropu" ve scene

    glRotatef(rotation1, 1.0, 0.0, 0.0)    # rotace objektu
    glRotatef(rotation2, 0.0, 1.0, 0.0)


@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers()
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_partial_disk()                    # vykresleni dratoveho modelu disku


pyglet.app.run()

13. Změna parametrů vykreslovaných kvadrik

Atributy kvadrik se nastavují před jejich vlastním vykreslením pomocí několika funkcí, které budou popsány v následujících odstavcích.

gluQuadricDrawStyle()

Funkcí gluQuadricDrawStyle() se nastavuje styl vykreslování kvadriky, tj. typ grafické primitivy, který bude použit pro reprezentaci povrchu kvadriky. Tato funkce má dva parametry. V prvním parametru quadric se specifikuje objekt kvadriky, který byl předem získán pomocí funkce gluNewQuadric(). Ve druhém parametru drawStyle se předává styl, kterým bude kvadrika vykreslena.

Kvadriku lze vykreslit pomocí jednotlivých bodů, úseček spojujících jednotlivé vrcholy nebo pomocí vyplněných polygonů:

GLU_FILL – kvadrika je vykreslena pomocí vyplněných polygonů.
GLU_LINE – povrch kvadriky je složen z úseček, výsledkem je tedy drátový (wireframe) model.
GLU_SILHOUETTE – povrch kvadriky je složen z úseček, ale pouze v těch částech povrchu, kde na sebe navazující plošky nejsou koplanární, tj. mají rozdílnou orientaci a směr svých normálových vektorů.
GLU_POINT – povrch kvadriky je složen z jednotlivých bodů.

Obrázek 19: Koule vykreslená pouze s využitím bodů.

gluQuadricNormals()

Funkcí gluQuadricNormals() se specifikuje, jakým způsobem se mají generovat normálové vektory na povrchu kvadriky. Normálové vektory se buď nemusí generovat vůbec, mohou se generovat pro každý polygon (použito u flat stínování) nebo samostatně pro každý vrchol (použito u Gouraudova stínování).

Tato funkce má dva parametry. V prvním parametru quadric se specifikuje objekt kvadriky, podobně jako u funkce gluQuadricDrawStyle().

Ve druhém parametru normal se pomocí symbolické konstanty předává způsob generování normálových vektorů. Tento parametr může nabývat tří hodnot:

GLU_NONE – normálové vektory nejsou generovány, není je tedy možné použít například při výpočtu osvětlení povrchu.
GLU_FLAT – normálové vektory jsou generovány pro každou vytvořenou plošku, při osvětlení má tedy každá ploška konstantní barvu, jelikož se používá konstantní stínování.
GLU_SMOOTH – normálové vektory jsou generovány pro každý vrchol (jsou tedy získány průměrem normálových vektorů jednotlivých plošek, které mají společný vrchol). Tento způsob vytváření normálových vektorů se používá zejména při Gouraudově stínování.

Obrázek 20: Koule vykreslená formou plošek (ovšem bez osvětlovacího modelu to není příliš viditelné).

gluQuadricOrientation()

Pomocí funkce gluQuadricOrientation() se nastavuje orientace normálových vektorů při vytváření kvadrik. Normálové vektory mohou být směřovány buď dovnitř tělesa nebo od povrchu tělesa směrem do volného prostoru. Tato funkce má opět dva parametry.

V prvním parametru quadric se specifikuje objekt kvadriky, podobně jako u výše popsaných funkcí gluQuadricDrawStyle() a gluQuadricNormals().

Ve druhém parametru orientation se specifikuje orientace vytvářených normálových vektorů. Tento parametr může nabývat následujících hodnot:

GLU_INSIDE – vytvářené normálové vektory budou směřovat dovnitř kvadriky.
GLU_OUTSIDE – vytvářené normálové vektory budou mířit směrem do prostoru. Toto chování je nastaveno implicitně a odpovídá smyslu normálových vektorů vytvářených pro účely osvětlování.

Obrázek 21: Koule vykreslená formou úseček (wireframe model).

gluQuadricTexture()

Funkcí gluQuadricTexture() se zakazuje nebo povoluje generování texturovacích souřadnic pro vytvářenou kvadriku. Ve druhém parametru této funkce se pomocí symbolických konstant GL_TRUE a GL_FALSE specifikuje, zda se mají souřadnice do textur generovat či nikoli. Implicitně je generování texturovacích souřadnic vypnuto, protože se jedná o poměrně zdlouhavou operaci.

Pokud se generování texturovacích souřadnic povolí, je pro každý vypočtený vrchol na povrchu kvadriky zavolána i funkce glTexCoord*() s příslušnou souřadnicí.

14. Šestý demonstrační příklad: vykreslení koule s interaktivní změnou všech parametrů modelu

Šestý příklad je nepatrně komplikovanější, protože je v něm možné několika klávesovými zkratkami změnit styl vykreslení koule:

Klávesa	Význam
P	vykreslení bodů na kouli
L	vykreslení drátového (wireframe) modelu
F	vykreslení plošek

PageUp	zvýšení počtu „rovnoběžek“
PageDown	snížení počtu „rovnoběžek“
Home	snížení počtu „poledníků“
End	zvýšení počtu „poledníků“

Obrázek 22: Snížením počtu „poledníků“ získáme těleso, které se již dokonalé kouli v žádném případě nepodobá.

Nastavení stylu vykreslování se provádí v nové funkci on_key_press(), která je volána ve chvíli, kdy uživatel stiskne klávesu (ovšem logiku pro rotaci těles zde nemáme, protože u ní potřebujeme zjistit, zda je klávesa stále stisknuta):

@window.event
def on_key_press(symbol, modifiers):
    global depthBufferEnabled
    global quadricDrawStyle
    global sphereSlices, sphereStacks

    if symbol == key.Z:
        depthBufferEnabled = not depthBufferEnabled
    if symbol == key.L:
        quadricDrawStyle = GLU_LINE
    if symbol == key.P:
        quadricDrawStyle = GLU_POINT
    if symbol == key.F:
        quadricDrawStyle = GLU_FILL
    if symbol == key.PAGEUP:
        sphereStacks += 1
    if symbol == key.PAGEDOWN:
        if sphereStacks > 1:
            sphereStacks -= 1
    if symbol == key.HOME:
        if sphereSlices > 1:
            sphereSlices -= 1
    if symbol == key.END:
        sphereSlices += 1

Úplný zdrojový kód příkladu vypadá následovně:

#!/usr/bin/env python

import pyglet
from pyglet.gl import *
from pyglet.window import key

fov = 70.0                                 # zorny uhel (field of view)
nearPlane = 0.1                            # blizsi orezavaci rovina
farPlane = 90.0                            # vzdalenejsi orezavaci rovina

r1 = 0.0
r2 = 0.0

depthBufferEnabled = False                 # povoleni ci zakaz Z-bufferu

quadricDrawStyle = GLU_LINE                # styl vykreslovani kvadriky
sphereSlices = 10                          # rozdeleni koule na 'poledniky'
sphereStacks = 10                          # rozdeleni koule na 'rovnobezky'


window = pyglet.window.Window(width=500,
                              height=500,
                              caption="Pyglet library")

keys = key.KeyStateHandler()


def init():
    glClearColor(0.0, 0.0, 0.3, 0.0)       # barva pozadi obrazku
    glPolygonMode(GL_FRONT, GL_FILL)       # nastaveni rezimu vykresleni modelu
    glPolygonMode(GL_BACK, GL_FILL)

    # zakaz odstranovani hran nebo sten podle jejich normal
    glDisable(GL_CULL_FACE)
    glDepthFunc(GL_LESS)                   # funkce pro testovani fragmentu

    glShadeModel(GL_SMOOTH)                # nastaveni stinovaciho rezimu
    glPointSize(3.0)


@window.event
def on_resize(width, height):
    init()
    glViewport(0, 0, width, height)        # viditelna oblast pres cele okno


def draw_quadric(drawStyle, slices, stacks):
    radius = 8.0
    quadric = gluNewQuadric()                   # vytvoreni kvadriky
    gluQuadricDrawStyle(quadric, drawStyle)     # nastaveni vlastnosti kvadriky
    gluQuadricNormals(quadric, GLU_SMOOTH)      # smer generovanych normal
    gluSphere(quadric, radius, slices, stacks)  # vykresleni kvadriky
    gluDeleteQuadric(quadric)                   # zruseni kvadriky


def set_depth_buffer(depthBufferEnabled):
    if depthBufferEnabled:
        glEnable(GL_DEPTH_TEST)
    else:
        glDisable(GL_DEPTH_TEST)


def clear_buffers(depthBufferEnabled):
    if depthBufferEnabled:
        # vymazani vsech bitovych rovin barvoveho bufferu i Z bufferu
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
    else:
        # vymazani vsech bitovych rovin barvoveho bufferu
        glClear(GL_COLOR_BUFFER_BIT)


def set_projection_matrix(fov, nearPlane, farPlane):
    # zacatek modifikace projekcni matice
    glMatrixMode(GL_PROJECTION)
    # vymazani projekcni matice (=identita)
    glLoadIdentity()
    gluPerspective(fov, 1.0, nearPlane, farPlane)


def set_modelview_matrix(rotation1, rotation2):
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()                       # nahrat jednotkovou matici

    gluLookAt(4.0, 6.0, 18.0,              # bod, odkud se kamera diva
              0.0, 2.0,  0.0,              # bod, kam se kamera diva
              0.0, 1.0,  0.0)              # poloha "stropu" ve scene

    glRotatef(rotation1, 1.0, 0.0, 0.0)    # rotace objektu
    glRotatef(rotation2, 0.0, 1.0, 0.0)


@window.event
def on_key_press(symbol, modifiers):
    global depthBufferEnabled
    global quadricDrawStyle
    global sphereSlices, sphereStacks

    if symbol == key.Z:
        depthBufferEnabled = not depthBufferEnabled
    if symbol == key.L:
        quadricDrawStyle = GLU_LINE
    if symbol == key.P:
        quadricDrawStyle = GLU_POINT
    if symbol == key.F:
        quadricDrawStyle = GLU_FILL
    if symbol == key.PAGEUP:
        sphereStacks += 1
    if symbol == key.PAGEDOWN:
        if sphereStacks > 1:
            sphereStacks -= 1
    if symbol == key.HOME:
        if sphereSlices > 1:
            sphereSlices -= 1
    if symbol == key.END:
        sphereSlices += 1


@window.event
def on_draw():
    global r1, r2

    if keys[key.LEFT]:
        r2 -= 2
    if keys[key.RIGHT]:
        r2 += 2
    if keys[key.UP]:
        r1 -= 2
    if keys[key.DOWN]:
        r1 += 2

    clear_buffers(depthBufferEnabled)
    set_depth_buffer(depthBufferEnabled)
    set_projection_matrix(fov, nearPlane, farPlane)
    set_modelview_matrix(r1, r2)
    draw_quadric(quadricDrawStyle, sphereSlices, sphereStacks)


window.push_handlers(keys)
pyglet.app.run()

Obrázek 23: Snížením počtu „rovnoběžek“ opět získáme těleso, které se již dokonalé kouli v žádném případě nepodobá.

15. Repositář s demonstračními příklady

Všechny dnes popsané demonstrační příklady byly uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý repositář. Pro jejich spuštění je nutné mít nainstalovanou jak knihovnu Pyglet, tak i podpůrné grafické knihovny OpenGL a GLU (což se většinou provede automaticky v rámci instalace balíčku s Pygletem, viz též úvodní díl tohoto seriálu):

Příklad	Odkaz
54_quadric_sphere.py	https://github.com/tisnik/presentations/blob/master/pyglet/54_quadric_sphere.py
55_quadric_cylinder.py	https://github.com/tisnik/presentations/blob/master/pyglet/55_quadric_cylinder.py
56_quadric_cone.py	https://github.com/tisnik/presentations/blob/master/pyglet/56_quadric_cone.py
57_disk.py	https://github.com/tisnik/presentations/blob/master/pyglet/57_disk.py
58_partial_disk.py	https://github.com/tisnik/presentations/blob/master/pyglet/58_partial_disk.py
59_guadric_sphere_style.py	https://github.com/tisnik/presentations/blob/master/pyglet/59_guadric_sphere_style.py

16. Funkce knihovny GLU popsané v tomto článku

V dnešním článku jsme se seznámili s následujícími jedenácti funkcemi knihovny GLU:

gluNewQuadric()
gluQuadricDrawStyle()
gluQuadricOrientation()
gluQuadricNormals()
gluQuadricTexture()
gluQuadricCallback()
gluDeleteQuadric()
gluSphere()
gluCylinder()
gluDisk()
gluPartialDisk()

17. Odkazy na Internetu

Pyglet: Module Hierarchy
https://pythonhosted.org/pyglet/api/module-tree.html
Learning Modern OpenGL
https://www.codeproject.com/articles/771225/learning-modern-opengl
OpenGL Utility Library
https://en.wikipedia.org/wiki/OpenGL_Utility_Library
GLU Specification
https://www.opengl.org/registry/doc/glu1.3.pdf
The Perlin noise math FAQ
https://mzucker.github.io/html/perlin-noise-math-faq.html
Perlin noise
https://en.wikipedia.org/wiki/Perlin_noise
Perlin Noise Generator (Python recipe)
http://code.activestate.com/recipes/578470-perlin-noise-generator/
Simplex noise demystified
http://www.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf
glTexEnv - příkaz OpenGL
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/glTexEnv.xml
glGetTexEnv - příkaz OpenGL
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/glGetTexEnv.xml
Pyglet Home Page
https://bitbucket.org/pyglet/pyglet/wiki/Home
Dokumentace k verzi 1.2
https://pyglet.readthedocs.io/en/pyglet-1.2-maintenance/
Dokumentace k verzi 1.2 ve formátu PDF
https://readthedocs.org/projects/pyglet/downloads/pdf/pyglet-1.2-maintenance/
PyOpenGL
http://pyopengl.sourceforge.net/
The #! magic, details about the shebang/hash-bang mechanism on various Unix flavours
https://www.in-ulm.de/~mascheck/various/shebang/
Shebang (Unix)
https://en.wikipedia.org/wiki/Shebang_%28Unix%29
Domovská stránka systému LÖVE
http://love2d.org/
Simple DirectMedia Layer (home page)
http://www.libsdl.org/
Simple DirectMedia Layer (Wikipedia)
https://en.wikipedia.org/wiki/Simple_DirectMedia_Layer
Seriál Grafická knihovna OpenGL
https://www.root.cz/serialy/graficka-knihovna-opengl/
Pyglet event loop
http://pyglet.readthedocs.io/en/latest/programming_guide/eventloop.html
Decorators I: Introduction to Python Decorators
http://www.artima.com/weblogs/viewpost.jsp?thread=240808
3D Programming in Python - Part 1
https://greendalecs.wordpress.com/2012/04/21/3d-programming-in-python-part-1/
A very basic Pyglet tutorial
http://www.natan.termitnjak.net/tutorials/pyglet_basic.html
Alpha blending
https://en.wikipedia.org/wiki/Alpha_compositing#Alpha_blending