Úvodník
Na předchozí článek, v němž jsme se seznámili se základními typy grafů dostupných v knihovně Matplotlib, dnes navážeme. Ukážeme si totiž způsob vykreslení sloupcových grafů, oblíbených koláčových grafů, práci s histogramy i některé pokročilejší techniky použité při změnách stylů vykreslování.
Obsah
2. Propojení naměřených či vypočtených bodů úsečkami
5. Sloupcový graf se dvěma skupinami sloupců
8. Změna stylu vykreslování koláčových grafů
9. Sloupcový graf se zobrazením odchylek (či chyb)
10. Pokročilejší nastavení způsobu vykreslení odchylek
11. Repositář s demonstračními příklady z předchozího článku
12. Repositář s demonstračními příklady z dnešního článku
1. Integrovaná vývojová prostředí ve Fedoře: vykreslování grafů s využitím knihoven Numpy a matplotlib (2.část)
Na předchozí článek, v němž jsme si popsali základní vlastnosti knihovny Matplotlib, zejména kombinaci možností této knihovny s knihovnou Numpy, dnes navážeme. Ukážeme si totiž, jakým způsobem je možné vykreslit další typy grafů, zejména sloupcové grafy s jedním polem vstupním dat, sloupcové grafy s větším množstvím polí se vstupními daty, sloupcové grafy se zobrazením odchylek (či chyb), histogramy a samozřejmě taktéž oblíbené, i když mnohdy spíše zneužívané koláčové grafy i jejich vylepšené varianty. Taktéž si ukážeme rozdíl mezi propojením naměřených či vypočtených hodnot úsečkami a grafem, na němž jsou jasně patrné „schodky“.
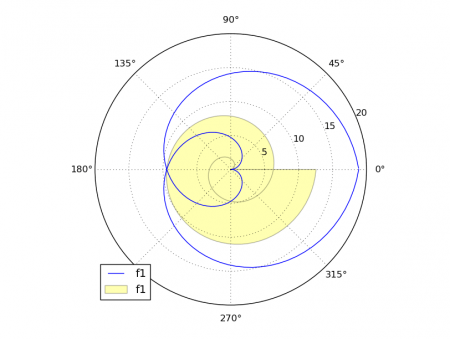
Obrázek 1: V předchozím článku jsme si mj. ukázali i způsob tvorby polárních grafů.
2. Propojení naměřených či vypočtených bodů úsečkami
Minule jsme se seznámili se dvěma typy grafů. Jednalo se především o snad vůbec nejběžnější typ grafu, v němž byly naměřené či vypočtené hodnoty pospojovány úsečkami, takže se vlastně pro celý průběh použila jediná lomená čára (polyčára). Jednou z možných modifikací tohoto typu grafu bylo vyplnění plochy pod vykreslenou lomenou čárou. Druhým typem grafu byl polární graf, který se vykresluje naprosto stejným způsobem (lomená čára popř. vyplněné segmenty pod touto čárou), ovšem při výpočtu jednotlivých bodů se namísto kartézských souřadnic používají souřadnice polární.
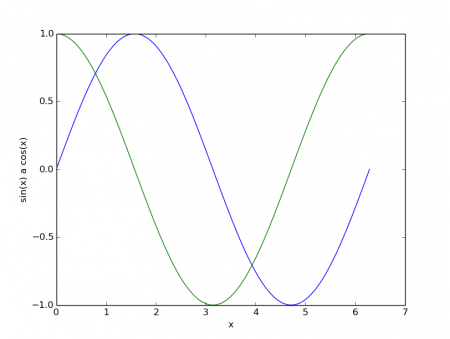
Obrázek 2: Graf, na němž jsou nakresleny průběhy dvou funkcí.
Pro připomenutí programové tvorby podobných grafů se podívejme na způsob vykreslení průběhu tří funkcí. Povšimněte si, že i když může mít rastrový či vektorový obrázek s grafem libovolnou velikost, je ve skutečnosti vypočteno pouze sto bodů každého průběhu a tyto body jsou následně pospojovány úsečkami. Vzhledem k tomu, že sto bodů je relativně vysoké číslo a samotné průběhy funkcí nevykazují velké změny (skoky apod.), vypadají všechny tři průběhy přirozeně, ovšem při snížení počtu bodů na pouhých deset se již ukazuje, jakým způsobem se graf vykresluje:
# Knihovny Numpy a matplotlib
#
# Dvanáctý demonstrační příklad:
# - vykreslení průběhu funkce sinc
# - při vykreslování se jednotlivé body spojí úsečkami
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0.2, 2*np.pi, 100)
# hodnoty na y-ové ose
y = np.sin(5*x)/x
y2 = 1/x
y3 = -y2
# vykreslit průběh funkce
plt.plot(x, y2, color='red', label='obalka sinc')
plt.plot(x, y3, color='red', label='obalka sinc')
plt.plot(x, y, color='blue', label='sinc(x)')
# povolení zobrazení mřížky
plt.grid(True)
# popis os
plt.xlabel("x")
plt.ylabel("sinc(x)")
# přidání legendy
plt.legend(loc="lower right")
# zobrazení grafu
plt.show()
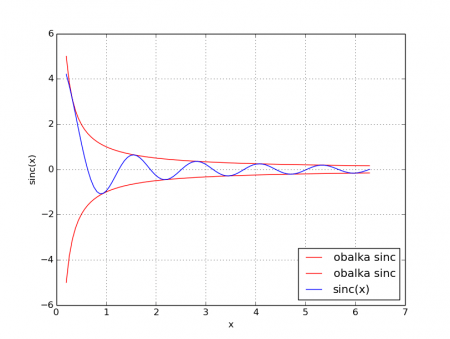
Obrázek 3: Vykreslení průběhu tří funkcí. Ve skutečnosti se však pro každou funkci vypočte pouze sto bodů, které jsou propojeny úsečkami. Díky velké hustotě bodů není (alespoň na těchto funkcích) náhrada hladkých křivek za lomenou čáru viditelné.
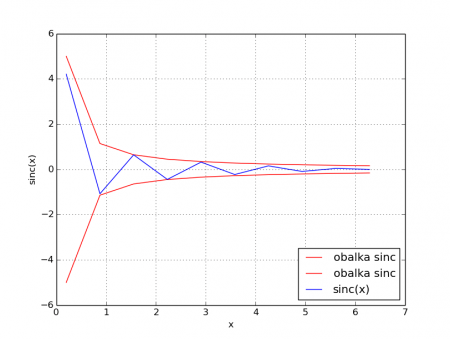
Obrázek 4: Pokud se počet vypočtených bodů sníží (zde na pouhých deset), je již jasně patrné, jakým způsobem byl graf vykreslen.
3. Graf používající „schodky“
V některých případech nám nemusí výše popsaný způsob vykreslení průběhů funkcí vyhovovat. Knihovna Matplotlib nám samozřejmě vychází vstříc, protože nabízí i další styly vykreslování, přičemž poměrně zajímavý a užitečný styl je založen na vykreslení „schodů“. Jedná se vlastně o přechodový typ grafu, v němž se sice stále vykresluje (spojitá) křivka, ovšem její tvar se již začíná podobat sloupcovému grafu (to je někdy poměrně důležité, protože můžeme naznačit například vzorkování apod.). Použití „schodků“ je vlastně velmi jednoduché, protože do příkazu pro vykreslení průběhu jedné funkce postačuje doplnit pojmenovaný parametr drawstyle a přiřadit mu hodnotu default:
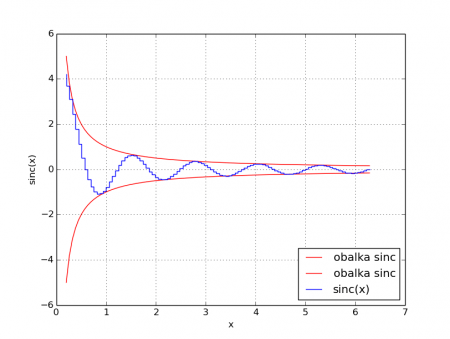
Obrázek 5: Zde se namísto lomené čáry použilo vykreslení průběhu funkcí se „schodky“.
Podívejme se na jednoduchý demonstrační příklad, v němž se v jednom grafu kombinují oba dva způsoby vykreslování – obálky funkce sinc jsou vykresleny lomenou čarou zatímco samotná funkce sinc je vykreslena s využitím „schodů“. Parametr drawstyle lze samozřejmě vynechat ve chvíli, kdy je mu přiřazena hodnota „default“:
# Knihovny Numpy a matplotlib
#
# Třináctý demonstrační příklad:
# - vykreslení průběhu funkce sinc
# - při vykreslování se použijí "schodky"
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0.2, 2*np.pi, 100)
# hodnoty na y-ové ose
y = np.sin(5*x)/x
y2 = 1/x
y3 = -y2
# vykreslit průběh funkce
plt.plot(x, y2, color='red', label='obalka sinc', drawstyle='default')
plt.plot(x, y3, color='red', label='obalka sinc', drawstyle='default')
plt.plot(x, y, color='blue', label='sinc(x)', drawstyle='steps')
# povolení zobrazení mřížky
plt.grid(True)
# popis os
plt.xlabel("x")
plt.ylabel("sinc(x)")
# přidání legendy
plt.legend(loc="lower right")
# zobrazení grafu
plt.show()
4. Jednoduchý sloupcový graf
Nyní se již dostáváme k dalšímu populárnímu a velmi často používanému typu grafu. Jedná se o sloupcový graf, přičemž sloupce (odpovídající naměřeným nebo vypočteným hodnotám) mohou být buď vodorovné nebo – a to častěji – svislé. Pro tvorbu sloupcového grafu se používají funkce matplotlib.pyplot.bar() (sloupce jsou svislé) popř. matplotlib.pyplot.barh() (sloupce jsou vodorovné). První dva parametry těchto funkcí jsou povinné – v obou případech se jedná o pole, přičemž první pole obsahuje x-ové souřadnice sloupců (většinou se tedy jedná o pole vytvořené příkazem numpy.arange(počet_prvků)) a pole druhé obsahuje výšky sloupců. Třetí parametr je nepovinný, ovšem poměrně důležitý, protože obsahuje relativní šířku sloupců. Tu můžeme zadat buď skalární hodnotou (což je obvyklé řešení) nebo taktéž pomocí pole. To znamená, že je možné vykreslit graf se sloupci, které mají rozdílnou šířku.
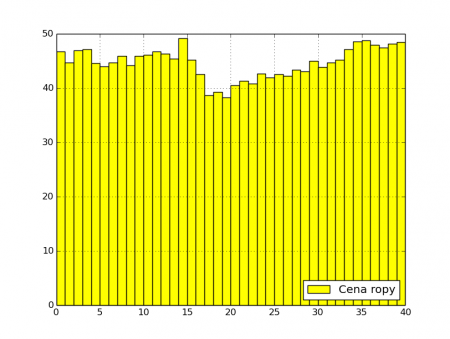
Obrázek 6: Sloupcový graf, v němž je šířka sloupců nastavena na hodnotu 1.0. Při této šířce se sloupce dotýkají.
Pro demonstrační příklad na vykreslení sloupcového grafu jsem vybral reálná data. Konkrétně se jedná o (v době vydaní článku již historické) ceny ropy uvedené v dolarech za barel. Při vykreslování byly funkci matplotlib.pyplot.bar() předány tři nepovinné parametry určující barvu výplně sloupců, barvu okrajů sloupců a popisek datové řady:
# Knihovny Numpy a matplotlib # # Čtrnáctý demonstrační příklad: # - jednoduchý sloupcový graf import numpy as np import matplotlib.pyplot as plt # historické ceny ropy cena_ropy = [ 46.68, 44.68, 46.90, 47.15, 44.59, 44.00, 44.63, 45.92, 44.15, 45.94, 46.05, 46.75, 46.25, 45.41, 49.20, 45.22, 42.56, 38.60, 39.31, 38.24, 40.45, 41.32, 40.80, 42.62, 41.87, 42.50, 42.23, 43.30, 43.08, 44.96, 43.87, 44.66, 45.15, 47.12, 48.52, 48.79, 47.98, 47.39, 48.14, 48.45] # počet prvků N = len(cena_ropy) # indexy prvků indexes = np.arange(N) # šířka sloupců width = 1.00 # sloupcový graf plt.bar(indexes, cena_ropy, width, color='yellow', edgecolor='black', label='Cena ropy') # povolení zobrazení mřížky plt.grid(True) # přidání legendy plt.legend(loc="lower right") # zobrazení grafu plt.show()
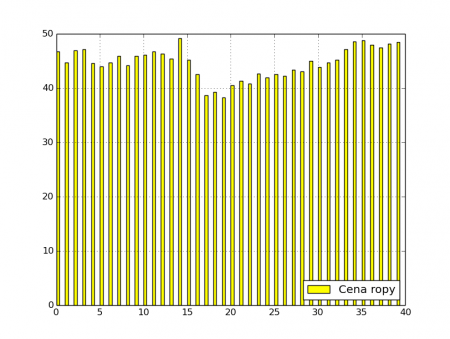
Obrázek 7: Sloupcový graf, v němž je šířka sloupců nastavena na hodnotu 0.3.
5. Sloupcový graf se dvěma skupinami sloupců
Podívejme se, co se stane ve chvíli, kdy se pokusíme do jediného grafu vykreslit dvě datové řady. Předpokládejme, že hodnoty první datové řady jsou uloženy v poli vals1, hodnoty řady druhé pak v poli pojmenovaném vals2. Indexy, tj. vlastně x-ové souřadnice sloupců, jsou shodné:
# první pole hodnot vals1 = [10, 15, 20, 12, 14, 8] # druhé pole hodnot vals2 = [19, 18, 6, 11, 6, 14] # počet prvků N = len(vals1) # indexy prvků indexes = np.arange(N) # sloupcový graf se dvěma skupinami sloupců plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1') # posunuté sloupce plt.bar(indexes, vals2, width, color='red', edgecolor='black', label='CPU#2')
Výsledkem je graf s překrývajícími se sloupci:
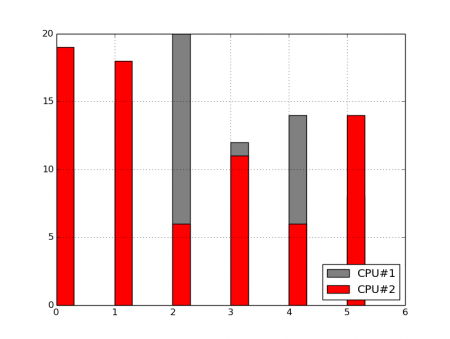
Obrázek 8: Sloupcový graf se dvěma datovými řadami ve chvíli, kdy jsou x-ové souřadnice sloupců shodné.
Graf z obrázku číslo 8 nám v mnoha případech pochopitelně nebude vyhovovat. Řešení je však jednoduché – postačuje posunout sloupce pro druhou (třetí, čtvrtou ...) řadu doprava. To se provede jednoduše přičtením skalární hodnoty k poli indexes. Proč toto řešení bude funkční již víme, neboť jsme si ve článku o knihovně Numpy řekli, že pro operace s poli (vektory, maticemi) byl přetížen operátor +, který zadanou skalární hodnotu přičte ke všem prvkům.
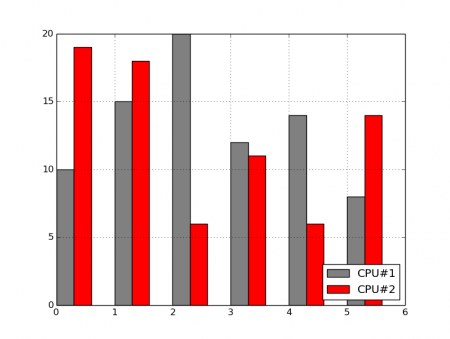
Obrázek 9: Sloupcový graf se dvěma datovými řadami ve chvíli, kdy jsou x-ové souřadnice druhé datové řady posunuty.
Úplný zdrojový kód demonstračního příkladu vypadá následovně:
# Knihovny Numpy a matplotlib # # Patnáctý demonstrační příklad: # - sloupcový graf se dvěma skupinami sloupců import numpy as np import matplotlib.pyplot as plt # první pole hodnot vals1 = [10, 15, 20, 12, 14, 8] # druhé pole hodnot vals2 = [19, 18, 6, 11, 6, 14] # počet prvků N = len(vals1) # indexy prvků indexes = np.arange(N) # šířka sloupců width = 0.30 # sloupcový graf se dvěma skupinami sloupců plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1') # posunuté sloupce plt.bar(indexes+width, vals2, width, color='red', edgecolor='black', label='CPU#2') # povolení zobrazení mřížky plt.grid(True) # přidání legendy plt.legend(loc="lower right") # zobrazení grafu plt.show()
6. Zobrazení histogramu
Dalším typem grafu, který je možné při použití knihovny Matplotlib použít, je histogram. Ten se vykresluje funkcí pojmenovanou logicky matplotlib.pyplot.hist(). Povinným parametrem jsou podle očekávání data, která se mají do histogramu vykreslit, ovšem funkce matplotlib.pyplot.hist() podporuje i další nepovinné parametry, zejména parametr normed řídicí normalizaci histogramu. Dalším mnohdy důležitým nepovinným parametrem je bins, jehož hodnotou se řídí šířka intervalů (tříd), tj. nepřímo počet sloupců v histogramu. Podívejme se na několik ukázek, z nichž bude použití nepovinného parametru bins patrné:
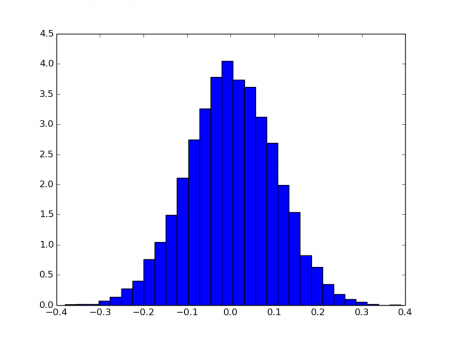
Obrázek 10: Histogram náhodných hodnot s normálním rozložením: parametr bins je nastaven na hodnotu 30.
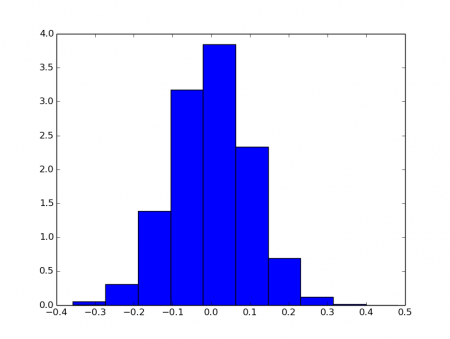
Obrázek 11: Histogram náhodných hodnot s normálním rozložením: parametr bins je nastaven na hodnotu 10.
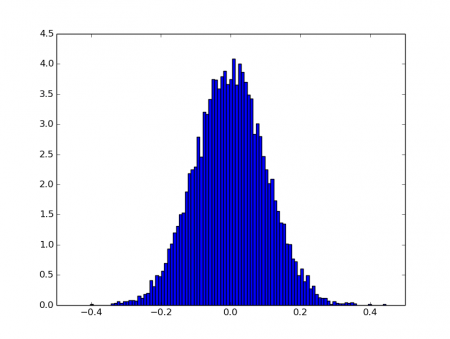
Obrázek 12: Histogram náhodných hodnot s normálním rozložením: parametr bins je nastaven na hodnotu 100.
Tyto histogramy byly vytvořeny následujícím programem:
# Knihovny Numpy a matplotlib # # Šestnáctý demonstrační příklad: # - jednoduchý histogram import numpy as np import matplotlib.pyplot as plt # náhodné hodnoty y = np.random.normal(0, 0.1, 10000) plt.hist(y, bins=30, range=None, normed=True) # zobrazení grafu plt.show()
7. Koláčový graf
Posledním typem grafu, s nímž se v dnešním článku seznámíme, jsou takzvané koláčové grafy, které již každý čtenář zcela jistě viděl. Tyto typy grafů se používají v případě, že nás nezajímají absolutní hodnoty, ale hodnoty relativní, konkrétně vzájemné poměry. Nejprve se podívejme, jak může koláčový graf vykreslený knihovnou Matplotlib vypadat. V grafu je zobrazeno zastoupení skriptovacích jazyků, přičemž nás nyní nezajímá, v kolika projektech se jednotlivé jazyky použily, ale jaké jsou poměry tohoto zastoupení:
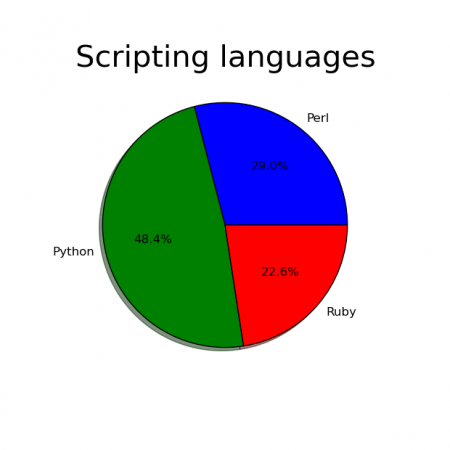
Obrázek 13: Koláčový graf zobrazující poměry mezi třemi hodnotami (zde konkrétně zastoupení skriptovacích jazyků).
Při vykreslení koláčového grafu můžeme použít přímo funkci matplotlib.pyplot.pie(), popř. lze použít podobný postup, jakým jsme minule vykreslili polární graf. Důležitý je především fakt, že koláčovému grafu můžeme předat pole s libovolnými hodnotami, nemusí se tedy jednat ani o procentuální poměry (se součtem 100%) ani o relativní hodnoty (se součtem 1.00). Knihovna Matplotlib si z předaných hodnot poměry vypočte automaticky. Dále si povšimněte použití nepovinného pojmenovaného parametru labels (s popisem jednotlivých výřezů) a parametru shadow, kterým se povoluje či zakazuje zobrazení 3D stínu:
# Knihovny Numpy a matplotlib
#
# Sedmnáctý demonstrační příklad:
# - koláčový graf
from matplotlib import pyplot as plt
from matplotlib import font_manager as fm
# make a square figure and axes
fig = plt.figure(1, figsize=(6,6), dpi=50)
ax = fig.add_axes([0.16, 0.16, 0.68, 0.68])
plt.title("Scripting languages")
ax.title.set_fontsize(30)
# popisky jednotlivých výřezů
labels = ['Perl', 'Python', 'Ruby']
# šířky jednotlivých výřezů
fracs = [90, 150, 70]
# vytvoření koláčového grafu
ax.pie(fracs, labels=labels, autopct='%1.1f%%', shadow=True)
# zobrazení grafu
plt.show()
8. Změna stylu vykreslování koláčových grafů
Koláčové grafy je samozřejmě možné upravovat. V této kapitole si ukážeme, jak se v grafu změní barvy jednotlivých výřezů a jak se jeden (nebo v případě potřeby i větší množství) výřezů „vysune“ od středové osy. Výsledkem bude následující obrázek:
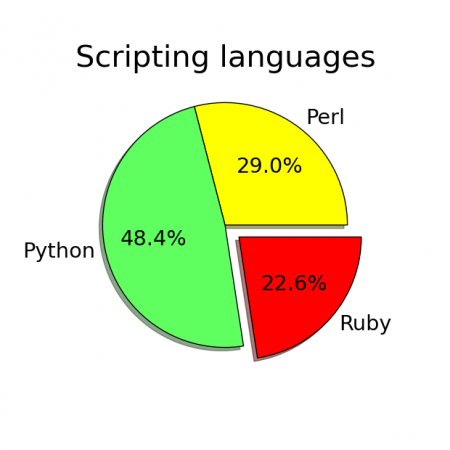
Obrázek 14: Změna stylu vykreslení koláčových grafů.
Změnu velikosti nadpisu zařizuje metoda set_fontsize(), změnu stylu písma pak kombinace set_size() společně s nastavením vlastností (properties) písma. Pravděpodobně nejdůležitější je však nepovinný parametr explode funkce matplotlib.pyplot.pie(), kterému se předá pole s relativními hodnotami určujícími míru vysunutí jednotlivých řezů:
# Knihovny Numpy a matplotlib
#
# Osmnáctý demonstrační příklad:
# - změna stylu koláčových grafů
from matplotlib import pyplot as plt
from matplotlib import font_manager as fm
# make a square figure and axes
fig = plt.figure(1, figsize=(6,6), dpi=50)
ax = fig.add_axes([0.16, 0.16, 0.68, 0.68])
plt.title("Scripting languages")
ax.title.set_fontsize(30)
# popisky jednotlivých výřezů
labels = ['Perl', 'Python', 'Ruby']
# šířky jednotlivých výřezů
fracs = [90, 150, 70]
# vytáhnutí výřezů
explode=(0.0, 0.0, 0.15)
# barvy
colors = ('yellow', '#60ff60', 'red')
# vytvoření koláčového grafu
patches, texts, autotexts = ax.pie(fracs, explode=explode, colors=colors, labels=labels, autopct='%1.1f%%', shadow=True)
# změna stylu písma
proptease = fm.FontProperties()
proptease.set_size('xx-large')
plt.setp(autotexts, fontproperties=proptease)
plt.setp(texts, fontproperties=proptease)
# zobrazení grafu
plt.show()
9. Sloupcový graf se zobrazením odchylek (či chyb)
Vraťme se ještě na chvíli ke sloupcovým grafům. V některých případech je nutné ke sloupcům přidat i povolené odchylky či chyby. I to je samozřejmě možné, a to díky existenci nepovinného pojmenovaného parametru yerr, kterému se předá buď skalární hodnota nebo pole o stejné délce, jakou má samotné vstupní pole hodnot. Podívejme se na způsob úpravy sloupcového grafu se dvěma datovými řadami o zobrazení odchylek. Tyto odchylky jsou uloženy v polích delta1 a delta2:
# Knihovny Numpy a matplotlib
#
# Devatenáctý demonstrační příklad:
# - sloupcový graf se dvěma skupinami sloupců
# a se zobrazením odchylek
import numpy as np
import matplotlib.pyplot as plt
# první pole hodnot a pole odchylek
vals1 = [10, 15, 20, 12, 14, 8]
delta1 = [1, 2, 3, 4, 5, 0]
# druhé pole hodnot a pole odchylek
vals2 = [19, 18, 6, 11, 6, 14]
delta2 = [4, 2, 3, 2, 2, 4]
# počet prvků
N = len(vals1)
# indexy prvků
indexes = np.arange(N)
# šířka sloupců
width = 0.30
# sloupcový graf se dvěma skupinami sloupců
plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1',
yerr=delta1)
# posunuté sloupce
plt.bar(indexes+width, vals2, width, color='red', edgecolor='black', label='CPU#2',
yerr=delta2)
# povolení zobrazení mřížky
plt.grid(True)
# přidání legendy
plt.legend(loc="lower right")
# zobrazení grafu
plt.show()
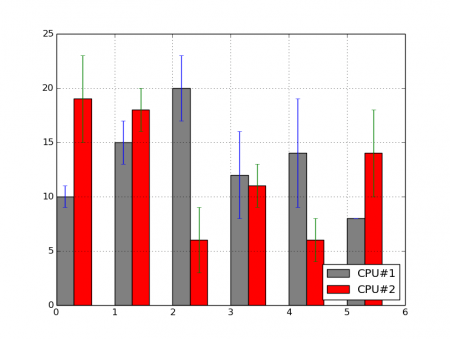
Obrázek 15: Sloupcový graf se zobrazením odchylek.
10. Pokročilejší nastavení způsobu vykreslení odchylek
Pokud budeme potřebovat změnit styl vykreslení odchylek/chyb, záhy zjistíme, že funkce matplotlib.pyplot.pie() nemá žádné povinné ani nepovinné parametry, které by bylo pro tento účel možné přímo použít! Ve skutečnosti se totiž všechny podobné parametry ukládají do slovníku (dictionary) předaného v pojmenovaném parametru error_kw. Podívejme se tedy, jak se změní barva a šířka úsečky vykreslených odchylek (přímo při vytváření slovníku ho i inicializujeme):
# Knihovny Numpy a matplotlib
#
# Dvacátý demonstrační příklad:
# - sloupcový graf se dvěma skupinami sloupců
# a se zobrazením odchylek
import numpy as np
import matplotlib.pyplot as plt
# první pole hodnot a pole odchylek
vals1 = [10, 15, 20, 12, 14, 8]
delta1 = [1, 2, 3, 4, 5, 0]
# druhé pole hodnot a pole odchylek
vals2 = [19, 18, 6, 11, 6, 14]
delta2 = [4, 2, 3, 2, 2, 4]
# počet prvků
N = len(vals1)
# indexy prvků
indexes = np.arange(N)
# šířka sloupců
width = 0.30
# sloupcový graf se dvěma skupinami sloupců
plt.bar(indexes, vals1, width, color='gray', edgecolor='black', label='CPU#1',
yerr=delta1, error_kw=dict(elinewidth=2,ecolor='red'))
# posunuté sloupce
plt.bar(indexes+width, vals2, width, color='red', edgecolor='black', label='CPU#2',
yerr=delta2, error_kw=dict(elinewidth=2,ecolor='black'))
# povolení zobrazení mřížky
plt.grid(True)
# přidání legendy
plt.legend(loc="lower right")
# zobrazení grafu
plt.show()
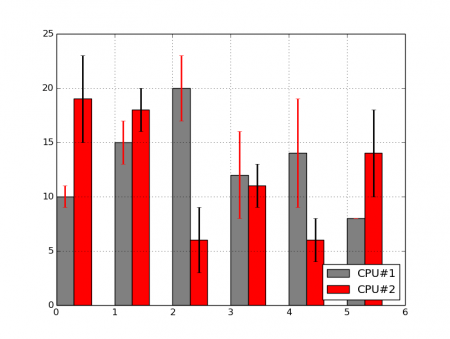
Obrázek 16: Změna stylu vykreslování odchylek (chyb).
11. Repositář s demonstračními příklady z předchozího článku
Všechny demonstrační příklady, s nimiž jsme se seznámili v předchozím i v dnešním článku, byly uloženy do Git repositáře umístěného na GitHubu (https://github.com/tisnik/presentations). Poslední verze zdrojových kódů naleznete pod odkazy uvedenými v tabulce pod tímto odstavcem. Začneme nejprve příklady, s nimiž jsme se seznámili již minule:
12. Repositář s demonstračními příklady z dnešního článku
Nyní nám pouze zbývá uvést odkazy na příklady popsané v dnešním článku:
13. Předchozí části seriálu
- Vývojová prostředí ve Fedoře (1. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-1-dil/ - Vývojová prostředí ve Fedoře (2. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-2-dil/ - Vývojová prostředí ve Fedoře (3. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-3-dil/ - Vývojová prostředí ve Fedoře (4. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-4-dil/ - Integrovaná vývojová prostředí ve Fedoře: PyDev
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Integrovaná vývojová prostředí ve Fedoře: PyDev (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: IPython a IPython Notebook
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-ipython-a-ipython-notebook/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: vykreslování grafů s využitím knihoven Numpy a matplotlib
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-vykreslovani-grafu-s-vyuzitim-knihoven-numpy-a-matplotlib/
14. Odkazy na Internetu
- Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Systémy lineárních rovnic
http://www.matematika.cz/systemy-linearnich-rovnic - IPython homepage
http://ipython.org/ - Dokumentace k IPythonu
http://ipython.org/documentation.html# - IPython Tutorial
http://ipython.readthedocs.org/en/stable/interactive/tutorial.html - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb - 0MQ Home Page
http://zeromq.org/ - Is IPython Notebook ever used as an IDE, or merely for presentations?
https://www.reddit.com/r/IPython/comments/1uk7hp/is_ipython_notebook_ever_used_as_an_ide_or_merely/ - The IDE as a Bad Programming Language Enabler
https://dzone.com/articles/ide-bad-programming-language - Enhanced Interactive Python with IPython
http://www.onlamp.com/pub/a/python/2005/01/27/ipython.html - Direct mode
https://en.wikipedia.org/wiki/Direct_mode - Seznámení s Python IDE Spyder (článek vyšel zde na mojefedora.cz)
http://mojefedora.cz/seznameni-s-python-ide-spyder/ - Stránka s popisem různých IDE pro Python
http://quintagroup.com/cms/python/ide - Eclipse (stránka o frameworku na Fedoraproject.org)
https://fedoraproject.org/wiki/Eclipse - PyDev (hlavní stránka)
http://pydev.sourceforge.net/index.html - PyDev (download, v podstatě není zapotřebí)
http://pydev.sourceforge.net/download.html - PyDev (stránka s metainformacemi o PyDev pluginu, použita v Eclipse)
http://www.pydev.org/updates/ - PyDev (stránka s pluginem, použita v Eclipse)
https://dl.bintray.com/fabioz/pydev/4.5.4/ - Certifikát, který lze do Eclipse doinstalovat
http://www.pydev.org/pydev_certificate.cer - PyDev FAQ
http://pydev.sourceforge.net/faq.html - PyDev (Wikipedia)
https://en.wikipedia.org/wiki/PyDev - Python (oficiální stránky projektu)
https://www.python.org/ - Jython
http://www.jython.org/ - IronPython
http://ironpython.net/ - Python 3.5.1 documentation
https://docs.python.org/3/ - PyDev: Unittest integration
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Continuous unit testing with Pydev (Python and Eclipse)
http://stackoverflow.com/questions/1015581/continuous-unit-testing-with-pydev-python-and-eclipse - Test-driven development
https://en.wikipedia.org/wiki/Test-driven_development


