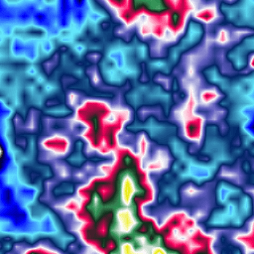
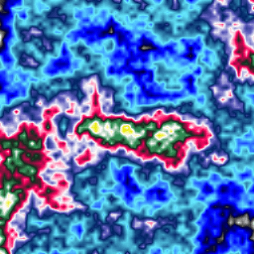
V desáté části seriálu o multimediální knihovně Pyglet si ukážeme způsob tvorby jednoduchých procedurálních textur, které je možné použít při vykreslování dvourozměrných a samozřejmě i trojrozměrných scén. Popisované textury budou založené na takzvaném moaré, dvourozměrné spektrální syntéze a taktéž na slavné Perlinově šumové funkci.
Obsah
1. Multimediální knihovna Pyglet – tvorba procedurálních textur
2. Moaré s kružnicovým vzorkem
3. První demonstrační příklad – základní moaré s kružnicovým vzorkem
4. Druhý demonstrační příklad – výběr barvové palety
5. Rozšíření repertoáru funkcí při tvorbě moaré
6. Třetí demonstrační příklad – použití dalších typů funkcí při tvorbě moaré
7. Algoritmy pro vykreslení textury „plasmy“
8. Dvourozměrná spektrální syntéza
9. Čtvrtý demonstrační příklad – použití dvourozměrné spektrální syntézy
10. Kompletní zdrojový kód čtvrtého demonstračního příkladu
13. Aplikace Perlinovy šumové funkce
14. Pátý demonstrační příklad – 2D textura vykreslená Perlinovou funkcí
15. Repositář s demonstračními příklady
1. Multimediální knihovna Pyglet – tvorba procedurálních textur
V předchozích částech tohoto seriálu jsme se zabývali problematikou texturování, konkrétně způsobem nanášení rastrových 2D textur na povrch vykreslovaných těles. Kromě textur uložených ve formě rastrových obrázků existuje i velmi dobře propracovaná technologie takzvaných procedurálních textur. Tyto textury jsou popsány matematickým výrazem, který každému bodu ležícímu v dvourozměrné ploše či v trojrozměrném prostoru přiřazuje jeho barvu, tj. jedná se (zjednodušeně řečeno) o funkci color=f(x,y) popř. color=f(x,y,z). Dnes se budeme zabývat prozatím poměrně jednoduchými procedurálními texturami: moaré, dvourozměrnou spektrální syntézou a Perlinovou šumovou funkcí.
Obrázek 1: Procedurální textura použitá pro vykreslení jednoduchého modelu planety.
2. Moaré s kružnicovým vzorkem
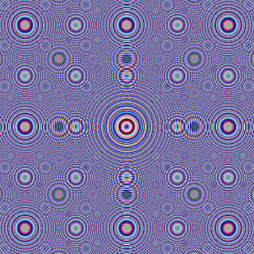
Velmi zajímavý a přitom jednoduše a současně i rychle vygenerovatelný vzorek založený na efektu takzvaného moaré vytvořil John Connett z Minnesotské univerzity. O tomto vzorku, který v podstatě názorně ukazuje vliv aliasu při tvorbě rastrových obrázků, později pojednal i A. K. Dewdney v časopise Scientific American. Tento vzorek je generovaný velmi jednoduchým způsobem: každému pixelu ve vytvářeném rastrovém obrázku (bitmapě) je přiřazena dvojice souřadnic [x, y]. Tyto souřadnice obecně neodpovídají celočíselným indexům pixelu, které můžeme například označit [i, j]. Posléze je pro každý pixel vypočtena hodnota z podle vztahu z=x2+y2. To je vše – pouze se na základě vypočtené hodnoty z vybere vhodná barva z barvové palety a pixel se obarví.
Obrázek 2: Moaré s kružnicovým vzorkem.
Tímto přímočarým, rychlým a jednoduchým způsobem je možné vytvářet mnohdy fantastické vzorky, pouze stačí měnit barvovou paletu (ideální jsou plynulé přechody mezi barvami – gradient) a měřítko, pomocí kterého se převádí celočíselné pozice pixelů v rastru [i, j] na souřadnice [x, y].
Obrázek 3: Mez zvětšení, při kterém již kružnicový vzorek začíná mizet.
To, že moaré s kružnicovým vzorkem netvoří fraktální strukturu (což z praktického hlediska znamená, že ho nelze libovolně zvětšovat, při určitém zvětšení textura zmizí), však nic nemění na tom, že se pomocí něho dají vytvářet zajímavé obrázky a textury, proto si jeho tvorbu podrobněji popíšeme v následujících dvou kapitolách. Praktická poznámka: pro 3D textury není tento vzorek vhodný, protože při různém pohledu na scénu (natáčení, přibližování apod.) dochází k několikanásobnému aliasu, který se projevuje nežádoucím poblikáváním a aplikace antialiasingu naopak může zcela vymazat původní detaily v textuře.
Obrázek 4: Při určitém měřítku narazíme na limit, pod kterým již nevidíme další detaily (viz střed obrázku, při jehož zvětšení již další detaily nebudou patrné).
3. První demonstrační příklad – základní moaré s kružnicovým vzorkem
Moaré s kružnicovým vzorkem je ukázáno v dnešním prvním demonstračním příkladu, který je založen na funkci nazvané recalc_circle_pattern(). Tato funkce provádí výpočet popsaný v předchozí kapitole, na konci pak převádí vypočtenou hodnotu do celočíselného rozsahu 0..255:
# Funkce provadejici vypocet moare s kruznicovym vzorkem
def recalc_circle_pattern(image, xmin, ymin, xmax, ymax):
width, height = image.size # rozmery obrazku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
print(xmin, xmax, ymin, ymax, width, height, stepx, stepy)
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
x1 += stepx
x2 = x1 * x1
y2 = y1 * y1
i = (int)(x2 + y2) & 255
color = (i, i, i)
image.putpixel((x, y), color)
y1 += stepy
Úplný zdrojový kód prvního příkladu vypadá následovně:
#!/usr/bin/env python
# Vytvoreni textury s "kruznicovym moare"
from PIL import Image
# textura by mela byt ctvercova a jeji sirka i vyska by mela byt
# mocninou cisla 2
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
# Funkce provadejici vypocet moare s kruznicovym vzorkem
def recalc_circle_pattern(image, xmin, ymin, xmax, ymax):
width, height = image.size # rozmery obrazku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
print(xmin, xmax, ymin, ymax, width, height, stepx, stepy)
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
x1 += stepx
x2 = x1 * x1
y2 = y1 * y1
i = (int)(x2 + y2) & 255
color = (i, i, i)
image.putpixel((x, y), color)
y1 += stepy
for i in range(0, 50, 10):
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
mez = (2 << 5) + i * 2.5
recalc_circle_pattern(image, -mez, -mez, mez, mez)
fileName = "patternA{index:02d}.png".format(index=i)
image.save(fileName)
Obrázek 5: Textura vygenerovaná prvním demonstračním příkladem.
Obrázek 6: Textura vygenerovaná prvním demonstračním příkladem.
Obrázek 7: Textura vygenerovaná prvním demonstračním příkladem.
Obrázek 8: Textura vygenerovaná prvním demonstračním příkladem.
Obrázek 9: Textura vygenerovaná prvním demonstračním příkladem.
4. Druhý demonstrační příklad – výběr barvové palety
Textury vykreslené ve stupních šedi sice mohou být pro některé projekty zajímavé (survival horory atd.), ovšem většinou požadujeme textury barevné. Ve skutečnosti je řešení jednoduché – postačuje ke každému vypočtenému indexu vybrat vhodnou barvu z barvové palety. Tradičně mají barvové palety 256 barev, ovšem samozřejmě je v případě potřeby možné vytvořit rozsáhlejší či naopak menší palety. Pro účely našich demonstračních příkladů použijeme textury získané z datových souborů programu Fractint a převedené na Pythonovské seznamy (viz též kapitolu číslo 15. Upravená funkce pro vytvoření textury bude vypadat následovně:
# Funkce provadejici vypocet moare s kruznicovym vzorkem
def recalc_circle_pattern(image, palette, xmin, ymin, xmax, ymax):
width, height = image.size # rozmery obrazku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
x1 += stepx
x2 = x1 * x1
y2 = y1 * y1
i = (int)(x2 + y2) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
y1 += stepy
Úplný zdrojový kód druhého příkladu vypadá následovně:
#!/usr/bin/env python
# Vytvoreni textury s "kruznicovym moare"
from PIL import Image
import palette_blues
import palette_greens
import palette_gold
import palette_ice
import palette_mandmap
# textura by mela byt ctvercova a jeji sirka i vyska by mela byt
# mocninou cisla 2
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
# Funkce provadejici vypocet moare s kruznicovym vzorkem
def recalc_circle_pattern(image, palette, xmin, ymin, xmax, ymax):
width, height = image.size # rozmery obrazku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
x1 += stepx
x2 = x1 * x1
y2 = y1 * y1
i = (int)(x2 + y2) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
y1 += stepy
mez = (2 << 5) + 50 * 2.5
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
image_pals = ((palette_blues.palette, "blues"),
(palette_greens.palette, "greens"),
(palette_gold.palette, "gold"),
(palette_ice.palette, "ice"),
(palette_mandmap.palette, "mandmap"))
for image_pal in image_pals:
print(image_pal[1])
recalc_circle_pattern(image, image_pal[0], -mez, -mez, mez, mez)
image.save("patternB_{name}.png".format(name=image_pal[1]))
Obrázek 10: Textura vygenerovaná druhým demonstračním příkladem.
Obrázek 11: Textura vygenerovaná druhým demonstračním příkladem.
5. Rozšíření repertoáru funkcí při tvorbě moaré
Předchozí dva demonstrační příklady je možné rozšířit o volbu dalších funkcí, které se použijí při výpočtu moaré. Výběr funkcí je takřka libovolný, pouze je žádoucí, aby při výpočtech docházelo k přetékání přes hodnotu 255 – tím vzniká požadovaný efekt tvořící základ vzorku. Některé níže uvedené „vhodné“ funkce je jsou vypsány v tabulce:
| Označení funkce | Tvar funkce |
|---|---|
| circle | zfactor×(x × x + y × y) |
| anticircle | zfactor×(x × x - y × y) |
| xyfun | zfactor×(x × x + xyfactor × x × y + y × y) |
| x3y3 | zfactor×(x × x × x + y × y × y) |
| x4y4 | zfactor×(x × x × x × x + y × y × y × y) |
| x3y3_xy | zfactor×(x × x × x + y × y × y) / (x × y) |
| xpy_xmy | zfactor×(x + y) / (x - y) |
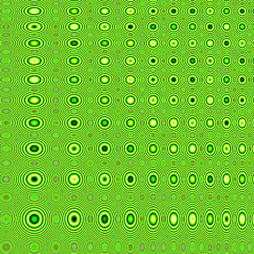
Obrázek 12: Moaré vypočtené s pomocí funkce nazvané x3y3.
Obrázek 13: Další možnosti tvorby moaré.
Obrázek 14: Další možnosti tvorby moaré.
6. Třetí demonstrační příklad – použití dalších typů funkcí při tvorbě moaré
Předchozí příklad nepatrně upravíme tak, že se namísto funkce recalc_circle_pattern() použije zobecněná funkce recalc_any_pattern(). Jedná se o funkci vyššího řádu, protože jejím posledním parametrem je jiná funkce použitá pro přepočet hodnot barev pixelů na základě jejich souřadnic. V Pythonu se předání jiné funkce provede snadno, a to konkrétně použitím anonymních funkcí (někdy nazývané lambda abstrakce nebo jen zkráceně lambdy):
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, <strong>lambda x,y : x*x + y*y</strong>)
Upravená forma funkce pro výpočet moaré se od původního kódu liší jen nepatrně:
# Funkce provadejici vypocet moare s kruznicovym ci jinym vzorkem
def recalc_any_pattern(image, palette, xmin, ymin, xmax, ymax, function):
width, height = image.size # rozmery obrazku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
x1 += stepx
val = function(x1, y1)
i = int(val) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
y1 += stepy
Úplný zdrojový kód třetího příkladu vypadá následovně:
#!/usr/bin/env python
# Vytvoreni textury s "kruznicovym moare" i dalsimi typy moare
from PIL import Image
import palette_blues
import palette_greens
import palette_gold
import palette_ice
import palette_mandmap
# textura by mela byt ctvercova a jeji sirka i vyska by mela byt
# mocninou cisla 2
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
# Funkce provadejici vypocet moare s kruznicovym vzorkem
def recalc_any_pattern(image, palette, xmin, ymin, xmax, ymax, function):
width, height = image.size # rozmery obrazku
stepx = (xmax - xmin)/width
stepy = (ymax - ymin)/height
y1 = ymin
for y in range(0, height):
x1 = xmin
for x in range(0, width):
x1 += stepx
val = function(x1, y1)
i = int(val) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
y1 += stepy
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
mez = (2 << 5) + 30 * 2.5
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, lambda x,y : x*x + y*y)
image.save("patternC_circle.png")
mez = (2 << 5) + 30 * 2.5
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, lambda x,y : x*x - y*y)
image.save("patternC_anticircle.png")
mez = 20.0
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, lambda x,y : x**3 + y**3)
image.save("patternC_x3y3.png")
mez = 20.0
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, lambda x,y : x**4 + y**4)
image.save("patternC_x4y4.png")
mez = 90.0
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, lambda x,y : x*x + y*y + x*y*1.5)
image.save("patternC_var1.png")
mez = 20.0
recalc_any_pattern(image, palette_mandmap.palette, -mez, -mez, mez, mez, lambda x,y : x*x*y + y*y*x)
image.save("patternC_var2.png")
Obrázek 15: Textura vykreslená třetím demonstračním příkladem.
Obrázek 16: Další textura vykreslená třetím demonstračním příkladem.
Obrázek 17: Další textura vykreslená třetím demonstračním příkladem.
7. Algoritmy pro vykreslení textury „plasmy“
V počítačové grafice, zejména v demech, byl velmi oblíbený efekt plasmy, ať už vykreslený jako statický obrázek, či animovaná sekvence postupně se měnící plasmy. Plasmu je možné vytvořit několika způsoby, typicky metodou rekurzivního dělení čtverce, Fourierovou syntézou či rekurzivním dělením plochy. Nejdříve si stručně popíšeme metodu rekurzivního dělení čtverce.
Obrázek 18: Klasická plasma, v níž jsou intenzity převedeny na stupně šedi.
Obrázek plasmy se v tomto případě generuje upraveným midpoint algoritmem (algoritmem posunu středního bodu) rozšířeného do dvourozměrného prostoru, přičemž čtverec je nahrazen rastrovým obrázkem (pro jednoduchost ve stupních šedi), kde pozice každého pixelu odpovídá souřadnicím bodu v rovině x-y a barva pixelu, tj. úroveň šedé, zbývající z-ové souřadnici bodu. Generování plasmy začíná v rozích rastrového obrázku a v jednotlivých krocích rekurze je obrázek dělen na čtvrtiny až do chvíle, kdy se dojde k velikosti jednoho pixelu, který se již dále samozřejmě nedělí. Kromě obrázků ve stupních šedi je možné generovat i barevné obrázky. Ty se tvoří dvojím způsobem – buď aplikací barvové palety, nebo vytvořením tří obrázků, z nichž každý odpovídá jednomu barvovému kanálu R, G, B – viz též následující obrázek.
Obrázek 19: Tři plasmy, každá vypočtená pro jednu barvovou složku (R, G, B).
Pomocí výše uvedené metody je možné vytvářet působivé obrázky plasmy; pro některé vstupní parametry však mohou být na obrázcích patrné vodorovné a svislé přechody mezi barvami, které tvoří hranice mezi čtverci na několika nejvyšších úrovních dělení. Na nižších úrovních, cca od čtvrté iterace, hranice splývají, neboť dochází ke snižování amplitudy odchylky Δ. Opticky rušivé přechody vznikají z toho důvodu, že se při každém rozdělení čtverce posune pouze jeho prostřední bod (střed) a nikoli prostřední body jeho hran – pro jejich posun nemáme dostatek informací, protože nevíme, jakým způsobem budou rozděleny čtyři sousední čtverce. Existuje několik způsobů, jak nežádoucí přechody odstranit. Některé způsoby spočívají v odlišném dělení čtverce, například střídavě po úhlopříčkách a vodorovných/svislých hranách, jiné způsoby zavádí „paměť“ posuvu prostředních bodů okolních čtverců apod.
Obrázek 20: Textura plasmy vygenerovaná třetím demonstračním příkladem.
Zajímavější (a poněkud neznámá) alternativní metoda, která už nespočívá v rekurzivním dělení čtverce, je založena na iterativním generování různě orientovaných přímek, které rozdělují obraz na dvě (obecně) nestejně velké poloviny. Po vygenerování náhodné přímky (ta po protnutí hranic obrázku vytvoří úsečku) se provedou následující operace:
- intenzita všech pixelů ležících nalevo od přímky se sníží o jedničku.
- intenzita všech pixelů ležících napravo od přímky se naopak o jedničku zvýší.
Pro vygenerování věrohodného obrázku plasmy je zapotřebí vytvoření přímky a snižování/zvyšování intenzity pixelů provádět v iterační smyčce mnohokrát, typická hodnota bývá 1 000 – 10 000 iterací. Po provedení takto vysokého množství iterací již hranice mezi různě orientovanými přímkami (resp. polorovinami) nejsou patrné. Po provedení všech iterací je nutné obrázek normalizovat, tj. nejnižší intenzitě pixelů (ta může být díky odčítání i záporná) přiřadit černou barvu a nejvyšší intenzitě barvu čistě bílou. Výsledkem těchto operací je plasma bez znatelných horizontálních či vertikálních hran.
Obrázek 21: Textura plasmy vygenerovaná třetím demonstračním příkladem.
8. Dvourozměrná spektrální syntéza
Spektrální syntéza je mimořádně vhodná pro použití v počítačové grafice, a to zejména z toho důvodu, že je ji možné relativně snadno rozšiřovat do více dimenzí (rozměrů). Pro jednorozměrný příklad je výsledkem křivka. Rozšíření do dvou dimenzí je jednoduché – výsledkem bude obrázek/textura plasmy a/nebo trojrozměrné výškové pole, které může představovat například model krajiny. Při použití tří dimenzí dostaneme jako výsledek trojrozměrnou mřížku, ve které jednotlivé objemové elementy (voxely) mohou představovat například hustotu prostoru v místě jejich výskytu. Tuto hustotu je posléze možné použít při generování reálně vypadajících modelů trojrozměrných oblak – to je velký rozdíl oproti oblakům vytvořených jako dvourozměrné textury, jejichž „dvojrozměrnost“ je při některých projekcích patrná.
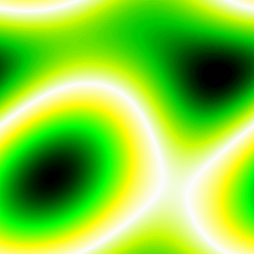
Obrázek 22: Textura plasmy vygenerovaná třetím demonstračním příkladem.
V případě dvourozměrné spektrální syntézy je fraktální dimenze výsledného obrázku rovna:
D=3-H
Přičemž hodnota takzvaného Hurstova exponentu H se pohybuje v rozsahu 0,0..1,0. Z toho vyplývá, že fraktální dimenze výsledné plasmy se pohybuje v rozsahu 2,0..3,0.
Pomocí těchto koeficientů je následně s využitím inverzní diskrétní Fourierovy transformace vypočten požadovaný obrázek plasmy:
X(x,y)=∑∑(A<sub>kl</sub>cos(kx+ly)+B<sub>kl</sub>sin(kx+ly))
Obrázek 23: Textura plasmy vygenerovaná třetím demonstračním příkladem.
9. Čtvrtý demonstrační příklad – použití dvourozměrné spektrální syntézy
V dnešním čtvrtém demonstračním příkladu je spektrální syntéza použita pro vygenerování textur, u nichž je možné zvolit vlastní barvovou paletu a taktéž míru náhodnosti textury. Ta se určuje dvěma parametry – hodnotou takzvaného Hurstova exponentu a taktéž počtem koeficientů spektrální syntézy. Čím větší zvolíte počet koeficientů, tím déle se bude plasma vykreslovat. V programu používáme knihovnu Numpy, s níž jsme se již na stránkách mojefedora.cz seznámili.
První pomocnou funkcí je funkce pro vygenerování náhodného čísla v rozsahu 0 až 1 s přibližným Gaussovým rozložením (ve skutečnosti tuto funkci najdeme i v knihovně, ale je dobré vědět, jak funkce pracuje):
def random_gauss():
'''
Vygenerovani nahodneho cisla v rozsahu 0..1 s pribliznym
Gaussovym rozlozenim
'''
N = 50
sum = 0.0
for i in range(N):
sum += random()
return sum/N
Další funkce již provádí vlastní syntézu. Funkci se předá obrázek, do něhož má být provedeno vykreslení, barvová paleta (seznam 256 trojic R, G, B), hodnota Hurstova exponentu a taktéž počet koeficientů spektrální syntézy. Celá funkce je rozdělena do tří částí. Nejprve se jedná o výpočet koeficientů Ak a Bk:
# h ... Hurstuv exponent
# n ... pocet koeficientu spektralni syntezy
def spectral_synthesis(image, palette, n, h):
width, height = image.size # rozmery obrazku
bitmap = np.zeros([height, width])
A = np.empty([n/2, n/2]) # koeficienty Ak
B = np.empty([n/2, n/2]) # koeficienty Bk
beta = 2.0 * h + 1 # promenna svazana s Hurstovym koeficientem
print("calculate coefficients")
# vypocet koeficientu Ak a Bk
for j in range(n/2):
for i in range(n/2):
rad_i = pow((i+1), -beta/2.0)*random_gauss()
rad_j = pow((j+1), -beta/2.0)*random_gauss()
phase_i = 2.0*math.pi*random()
phase_j = 2.0*math.pi*random()
A[j][i] = rad_i*math.cos(phase_i)*rad_j*math.cos(phase_j)
B[j][i] = rad_i*math.sin(phase_i)*rad_j*math.sin(phase_j)
Dále se vygeneruje plasma do pomocného dvourozměrného pole bitmap:
# vygenerovani plasmy
for j in range(height):
for i in range(width):
z = 0
# inverzni Fourierova transformace
for k in range(n/2):
for l in range(n/2):
u = (i-n/2)*2.0*math.pi/width
v = (j-n/2)*2.0*math.pi/height
z += A[k][l]*math.cos(k*u+l*v)+B[k][l]*math.sin(k*u+l*v)
bitmap[j][i] = z
Posléze je nutné najít maximální a minimální hodnotu v poli bitmap, přepočítat hodnoty tak, aby byly v rozsahu 0..255 a provést převod pole na obrázek (s aplikací barvové palety):
def compute_min_max(bitmap, width, height):
# pro prepocet intenzit pixelu
min = float("inf")
max = float("-inf")
# ziskani statistiky o obrazku - minimalni a maximalni hodnoty
for j in range(height):
for i in range(width):
z = bitmap[j][i]
if max < z:
max = z
if min > z:
min = z
return min, max
def convert_to_image(bitmap, image, width, height, palette):
print("contrast adjustment")
min, max = compute_min_max(bitmap, width, height)
k = 255.0 / (max - min)
# zmena kontrastu a kopie bitmapy
for y in range(height):
for x in range(width):
f = float(bitmap[y][x])
f -= min
f *= k
i = int(f) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
Obrázek 24: Textura plasmy vygenerovaná třetím demonstračním příkladem.
10. Kompletní zdrojový kód čtvrtého demonstračního příkladu
V předchozí kapitole jsme si popsali nejdůležitější části čtvrtého příkladu. Jeho kompletní zdrojový kód vypadá následovně:
#!/usr/bin/env python
# Vytvoreni textury typu "plasma"
from PIL import Image
from random import random
import palette_blues
import palette_greens
import palette_gold
import palette_ice
import palette_mandmap
import numpy as np
import math
# textura by mela byt ctvercova a jeji sirka i vyska by mela byt
# mocninou cisla 2
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
def random_gauss():
'''
Vygenerovani nahodneho cisla v rozsahu 0..1 s pribliznym
Gaussovym rozlozenim
'''
N = 50
sum = 0.0
for i in range(N):
sum += random()
return sum/N
def compute_min_max(bitmap, width, height):
# pro prepocet intenzit pixelu
min = float("inf")
max = float("-inf")
# ziskani statistiky o obrazku - minimalni a maximalni hodnoty
for j in range(height):
for i in range(width):
z = bitmap[j][i]
if max < z:
max = z
if min > z:
min = z
return min, max
def convert_to_image(bitmap, image, width, height, palette):
print("contrast adjustment")
min, max = compute_min_max(bitmap, width, height)
k = 255.0 / (max - min)
# zmena kontrastu a kopie bitmapy
for y in range(height):
for x in range(width):
f = float(bitmap[y][x])
f -= min
f *= k
i = int(f) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
# h ... Hurstuv exponent
# n ... pocet koeficientu spektralni syntezy
def spectral_synthesis(image, palette, n, h):
width, height = image.size # rozmery obrazku
bitmap = np.zeros([height, width])
A = np.empty([n/2, n/2]) # koeficienty Ak
B = np.empty([n/2, n/2]) # koeficienty Bk
beta = 2.0 * h + 1 # promenna svazana s Hurstovym koeficientem
print("calculate coefficients")
# vypocet koeficientu Ak a Bk
for j in range(n/2):
for i in range(n/2):
rad_i = pow((i+1), -beta/2.0)*random_gauss()
rad_j = pow((j+1), -beta/2.0)*random_gauss()
phase_i = 2.0*math.pi*random()
phase_j = 2.0*math.pi*random()
A[j][i] = rad_i*math.cos(phase_i)*rad_j*math.cos(phase_j)
B[j][i] = rad_i*math.sin(phase_i)*rad_j*math.sin(phase_j)
print("plasma synthesis")
# vygenerovani plasmy
for j in range(height):
for i in range(width):
z = 0
# inverzni Fourierova transformace
for k in range(n/2):
for l in range(n/2):
u = (i-n/2)*2.0*math.pi/width
v = (j-n/2)*2.0*math.pi/height
z += A[k][l]*math.cos(k*u+l*v)+B[k][l]*math.sin(k*u+l*v)
bitmap[j][i] = z
convert_to_image(bitmap, image, width, height, palette)
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
spectral_synthesis(image, palette_greens.palette, 4, 0.5)
image.save("patternD_plasma1.png")
spectral_synthesis(image, palette_blues.palette, 10, 0.5)
image.save("patternD_plasma2.png")
spectral_synthesis(image, palette_mandmap.palette, 5, 0.1)
image.save("patternD_plasma3.png")
spectral_synthesis(image, palette_mandmap.palette, 5, 1.0)
image.save("patternD_plasma4.png")
spectral_synthesis(image, palette_gold.palette, 15, 0.5)
image.save("patternD_plasma5.png")
spectral_synthesis(image, palette_ice.palette, 15, 0.8)
image.save("patternD_plasma6.png")
Obrázek 25: Textura plasmy vygenerovaná třetím demonstračním příkladem.
11. Perlinova šumová funkce
Další způsob tvorby procedurálních textur je založena na takzvané Perlinově šumové funkci. Perlinova šumová funkce byla s velkým úspěchem použita v mnoha aplikacích počítačové grafiky; například prakticky každý film, ve kterém je použita renderovaná grafika, tuto funkci nějakým způsobem použil. Její úspěch spočívá v tom, že se pomocí ní dají do původně přesných a "počítačově chladných" modelů vnést náhodné prvky, takže se model či celá vytvářená scéna přiblíží realitě. Podobný princip vnesení náhodnosti ostatně umožňují i fraktály, zejména ty vytvářené na stochastickém základě (plasma, stochastické L-systémy apod.). Perlin šumovou funkci navrhl už v roce 1983, v roce 1985 o její aplikaci vznikl článek prezentovaný na SIGGRAPHu (jedna z nejvýznamnějších konferencí počítačové grafiky) a v letech 1986 až 1988 tuto funkci s některými modifikacemi používaly takové firmy, jako Pixar, Alias, SoftImage apod.
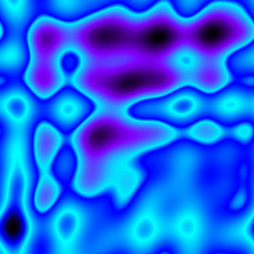
Obrázek 26: Perlinova šumová funkce použitá při generování dvourozměrných textur.
12. Princip šumové funkce
Při tvorbě textur, které by měly reprezentovat přírodní vzorky, jako je mramor, dřevo či mraky, není možné použít ani klasický generátor pseudonáhodných čísel RNG (tím je myšlena například například rand() ze standardní céčkové knihovny), ale ani základní matematické funkce. V minulosti byly prováděny pokusy o využití goniometrických funkcí, které posléze vyústily v úspěšnou metodu generování plasmy pomocí Fourierovy syntézy, což je téma, kterému jsme se věnovali výše. Při přímé aplikaci generátorů pseudonáhodných čísel sice získáme šum, ten je však příliš náhodný a vůbec se nehodí pro generování textur, a to ani po své filtraci.
Obrázek 27: Jednorozměrná Perlinova šumová funkce s parametry alpha=2, beta=2, n=10.
Perlin pro účely vytváření přírodních textur navrhl výpočet, který sice využívá generátor pseudonáhodných čísel, ale mezi jednotlivými vypočtenými náhodnými hodnotami je prováděna interpolace, která výsledný průběh funkce vyhladí, takže se již nebude jednat o zcela náhodný šum. Pro vyhlazení je možné použít velké množství matematických funkcí, od jednoduché lineární interpolace přes kvadratické a kubické funkce až po funkce goniometrické a jejich vzájemné kombinace. Perlin použil (pokud celý popis jeho postupu značně zjednodušíme) dvojici funkcí, první nazvanou s_curve() a druhou nazvanou lerp(). Při výpočtu šumu je nejdříve použita funkce s_curve(), posléze se získají dvě náhodné hodnoty a na výsledek je aplikována funkce lerp(). Funkce s_curve() má tvar:
s_curve(t)=(t2*(3-2t))
Obrázek 28: Průběh funkce s_curve(); na horizontální ose je použito jiné měřítko, než v originálních Perlinových zdrojových kódech. Ve skutečnosti je v praxi využit pouze rozsah vstupních hodnot 0..1 (na grafu 0..20), sestupná část již nikoli.
Funkce lerp() má tvar:
lerp(t, a, b)=(a+t(b-a))
Všimněte si, že se v tomto případě nejedná o nic jiného, než o lineární interpolaci řízenou parametrem t. Pro t=0,0 je výsledkem funkce hodnota a, pro t=1,0 pak hodnota b. Konkrétní hodnota parametru t je získána výpočtem výše uvedené funkce s_curve().
13. Aplikace Perlinovy šumové funkce
Perlinovu šumovou funkci je možné v počítačové grafice všestranně použít k vytváření mnoha různých přírodních vzorků, například mramoru, textury dřeva, ohně, mraků, kamenů hor atd. atd. Všechny výše uvedené funkce je možné různými způsoby modifikovat, například do výpočtů prováděných ve funkcích PerlinNoise1D() a PerlinNoise2D přidávat další matematické funkce. Často se původní Perlinova funkce upravuje tak, že se sčítají absolutní hodnoty dílčích šumů (což budeme používat i my v demonstračním příkladu), přidává se goniometrická funkce sinus atd.
Obrázek 29: Textura vytvořená pomocí Perlinovy funkce pátým příkladem.
Mnohem důležitější je však rozšíření výpočtů do trojrozměrného prostoru. Programově se nejedná o žádnou komplikaci (viz snadný a přímočarý přechod z 1D na 2D), ovšem dopad na možnosti využití je značný. Dvourozměrné textury mají několik vážných nevýhod, z nichž ta největší spočívá v obtížném mapování na nerovné povrchy. Například mapování obdélníkové textury na kouli vede k tomu, že se textura na pólech smrští a naopak na rovníku příliš roztáhne. Výsledek je většinou neuspokojivý, zvláště při aplikaci šumové funkce (ta by měla být směrově invariantní). Přechodem k výpočtům 3D (volumetrických) textur se tohoto problému zbavíme (viz obrázek číslo 1 zobrazený v úvodní kapitole), protože pro každý bod v prostoru je možné zjistit hodnotu šumu bez nutnosti mapování.
Obrázek 30: Textura vytvořená pomocí Perlinovy funkce pátým příkladem.
3D textury se často používají v raytracerech, kde se projevuje i jejich další přednost – jejich hodnotu je možné vypočítat pro libovolný bod v prostoru, není tedy nutné nejprve provést výpočet textury v nějakém rastru. Tím ušetříme velké množství paměti (3D rastrové textury mají obrovské paměťové nároky), nebude docházet k aliasu a také je možné texturu animovat, například postupnou změnou některého z parametrů (barvové palety, parametru alpha, beta, n atd.)
Obrázek 31: Textura vytvořená pomocí Perlinovy funkce pátým příkladem.
14. Pátý demonstrační příklad – 2D textura vykreslená Perlinovou funkcí
V pátém a současně i dnešním posledním příkladu si ukážeme způsob vytvoření jednoduché textury pomocí Perlinovy šumové funkce. I tento příklad je rozdělen na několik částí a pomocných funkcí. Například funkce random_array() vrátí dvourozměrné pole náhodných hodnot o specifikované amplitudě:
def random_array(width, height, amplitude):
return [[random() * amplitude for i in range(width)]
for j in range(height)]
Nejdůležitější částí je funkce nazvaná perlin_noise(), která postupně (pro specifikovaný počet „oktáv“) vytvoří pole náhodných hodnot a posléze mezi nimi provede interpolaci. Pole náhodných hodnot se postupně zvětšuje (v obou směrech), takže čím více oktáv je zadaných, tím náhodnější výsledná textura bude:
def perlin_noise(image, palette, noise, octaves):
width, height = image.size # rozmery obrazku
bitmap = np.zeros([height, width])
# postupne vytvoreni 'octaves' vrstev v obrazku
for k in range(octaves):
size = 2 ** k + 1
amplitude = noise ** k
# vytvoreni pole nahodnych cisel o dane amplidude
array = random_array(size, size, amplitude)
n = width / float(size-1.0)
# interpolace hodnot v poli nahodnych cisel
for y in range(height):
for x in range(width):
i = int(x / n) # prepocet mezi pozici pixelu a indexem v poli
j = int(y / n)
x0 = x - i * n
x1 = n - x0
y0 = y - j * n
y1 = n - y0
# interpolace
z = array[j][i] * x1 * y1
z += array[j][i + 1] * x0 * y1
z += array[j + 1][i] * x1 * y0
z += array[j + 1][i + 1] * x0 * y0
z /= n * n
bitmap[y][x] += z
Kompletní zdrojový kód tohoto příkladu vypadá takto (opět je použita knihovna Numpy):
#!/usr/bin/env python
# Perlinuv sum
from PIL import Image
from random import random
import palette_blues
import palette_greens
import palette_gold
import palette_ice
import palette_mandmap
import numpy as np
import math
# textura by mela byt ctvercova a jeji sirka i vyska by mela byt
# mocninou cisla 2
IMAGE_WIDTH = 256
IMAGE_HEIGHT = 256
def compute_min_max(bitmap, width, height):
# pro prepocet intenzit pixelu
min = float("inf")
max = float("-inf")
# ziskani statistiky o obrazku - minimalni a maximalni hodnoty
for j in range(height):
for i in range(width):
z = bitmap[j][i]
if max < z:
max = z
if min > z:
min = z
return min, max
def convert_to_image(bitmap, image, width, height, palette):
print("contrast adjustment")
min, max = compute_min_max(bitmap, width, height)
k = 255.0 / (max - min)
# zmena kontrastu a kopie bitmapy
for y in range(height):
for x in range(width):
f = float(bitmap[y][x])
f -= min
f *= k
i = int(f) & 255
color = (palette[i][0], palette[i][1], palette[i][2])
image.putpixel((x, y), color)
def random_array(width, height, amplitude):
return [[random() * amplitude for i in range(width)]
for j in range(height)]
def perlin_noise(image, palette, noise, octaves):
width, height = image.size # rozmery obrazku
bitmap = np.zeros([height, width])
# postupne vytvoreni 'octaves' vrstev v obrazku
for k in range(octaves):
size = 2 ** k + 1
amplitude = noise ** k
# vytvoreni pole nahodnych cisel o dane amplidude
array = random_array(size, size, amplitude)
n = width / float(size-1.0)
# interpolace hodnot v poli nahodnych cisel
for y in range(height):
for x in range(width):
i = int(x / n) # prepocet mezi pozici pixelu a indexem v poli
j = int(y / n)
x0 = x - i * n
x1 = n - x0
y0 = y - j * n
y1 = n - y0
# interpolace
z = array[j][i] * x1 * y1
z += array[j][i + 1] * x0 * y1
z += array[j + 1][i] * x1 * y0
z += array[j + 1][i + 1] * x0 * y0
z /= n * n
bitmap[y][x] += z
convert_to_image(bitmap, image, width, height, palette)
image = Image.new("RGB", (IMAGE_WIDTH, IMAGE_HEIGHT))
perlin_noise(image, palette_mandmap.palette, 0.7, 6)
image.save("patternE_perlin_noise1.png")
perlin_noise(image, palette_mandmap.palette, 0.7, 7)
image.save("patternE_perlin_noise2.png")
perlin_noise(image, palette_blues.palette, 0.7, 9)
image.save("patternE_perlin_noise3.png")
perlin_noise(image, palette_gold.palette, 0.7, 11)
image.save("patternE_perlin_noise4.png")
perlin_noise(image, palette_greens.palette, 0.3, 12)
image.save("patternE_perlin_noise5.png")
Obrázek 32: Textura vytvořená pomocí Perlinovy funkce pátým příkladem.
15. Repositář s demonstračními příklady
Všechny dnes popsané demonstrační příklady byly uloženy do Git repositáře dostupného na adrese https://github.com/tisnik/presentations. Příklady si můžete v případě potřeby stáhnout i jednotlivě bez nutnosti klonovat celý repositář. Pro jejich spuštění je nutné mít nainstalovanou jak knihovnu Pyglet, tak i podpůrné grafické knihovny OpenGL a GLU (což se většinou provede automaticky v rámci instalace balíčku s Pygletem, viz též úvodní díl tohoto seriálu):
| Příklad | Odkaz |
|---|---|
| 49_circle_moire.py | https://github.com/tisnik/presentations/blob/master/pyglet/49_circle_moire.py |
| 50_circle_moire_with_palette.py | https://github.com/tisnik/presentations/blob/master/pyglet/50_circle_moire_with_palette.py |
| 51_more_patterns.py | https://github.com/tisnik/presentations/blob/master/pyglet/51_more_patterns.py |
| 52_plasma.py | https://github.com/tisnik/presentations/blob/master/pyglet/52_plasma.py |
| 53_perlin.py | https://github.com/tisnik/presentations/blob/master/pyglet/53_perlin.py |
Dalších pět souborů obsahuje deklaraci barvových palet:
Obrázek 33: Textura vytvořená pomocí Perlinovy funkce pátým příkladem.
16. Odkazy na Internetu
- The Perlin noise math FAQ
https://mzucker.github.io/html/perlin-noise-math-faq.html - Perlin noise
https://en.wikipedia.org/wiki/Perlin_noise - Perlin Noise Generator (Python recipe)
http://code.activestate.com/recipes/578470-perlin-noise-generator/ - Simplex noise demystified
http://www.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf - glTexEnv - příkaz OpenGL
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/glTexEnv.xml - glGetTexEnv - příkaz OpenGL
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/glGetTexEnv.xml - Pyglet Home Page
https://bitbucket.org/pyglet/pyglet/wiki/Home - Dokumentace k verzi 1.2
https://pyglet.readthedocs.io/en/pyglet-1.2-maintenance/ - Dokumentace k verzi 1.2 ve formátu PDF
https://readthedocs.org/projects/pyglet/downloads/pdf/pyglet-1.2-maintenance/ - PyOpenGL
http://pyopengl.sourceforge.net/ - The #! magic, details about the shebang/hash-bang mechanism on various Unix flavours
https://www.in-ulm.de/~mascheck/various/shebang/ - Shebang (Unix)
https://en.wikipedia.org/wiki/Shebang_%28Unix%29 - Domovská stránka systému LÖVE
http://love2d.org/ - Simple DirectMedia Layer (home page)
http://www.libsdl.org/ - Simple DirectMedia Layer (Wikipedia)
https://en.wikipedia.org/wiki/Simple_DirectMedia_Layer - Seriál Grafická knihovna OpenGL
https://www.root.cz/serialy/graficka-knihovna-opengl/ - Pyglet event loop
http://pyglet.readthedocs.io/en/latest/programming_guide/eventloop.html - Decorators I: Introduction to Python Decorators
http://www.artima.com/weblogs/viewpost.jsp?thread=240808 - 3D Programming in Python - Part 1
https://greendalecs.wordpress.com/2012/04/21/3d-programming-in-python-part-1/ - A very basic Pyglet tutorial
http://www.natan.termitnjak.net/tutorials/pyglet_basic.html - Alpha blending
https://en.wikipedia.org/wiki/Alpha_compositing#Alpha_blending