Na předchozí článek pojednávající o integrovaných vývojových prostředích, v němž jsme se zmiňovali především o IPythonu a taktéž o IPython Notebooku, dnes tematicky navážeme, protože si ukážeme, jakým způsobem je možné využít IPython Notebook společně s knihovnou Numpy. Tyto dva nástroje, pokud jsou navíc v případě potřeby doplněny o knihovnu SciPy a Matplotlib, mohou v mnoha oblastech zdárně konkurovat i komerčním nástrojům typu Matlab či Maple.
Obsah
1. Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
2. Základy, na nichž je postavena knihovna Numpy
3. Datové typy prvků, z nichž jsou tvořena pole
9. Přetypování všech prvků v poli
10. Zjištění tvaru pole pomocí funkce numpy.shape
11. Změna tvarů polí s využitím funkce numpy.reshape
12. Vliv nepovinného parametru „order“ na (zdánlivou) změnu tvaru pole
1. Integrovaná vývojová prostředí ve Fedoře: praktické použití IPythonu a knihovny Numpy
V minulé části seriálu o integrovaných vývojových prostředích, která jsou dostupná (nejenom) pro vývojáře pracující ve Fedoře, jsme se zaměřili na popis nástrojů nazvaných IPython a IPython Notebook. Připomeňme si ve stručnosti, že se sice nejedná o „klasická“ integrovaná vývojová prostředí typu Eclipse či Visual Studio, ale o nástroje, které díky použití smyčky REPL (IPython) či konceptu takzvaných diářů (IPython Notebook) umožňují, aby uživatelé vytvářeli aplikace či jen prováděli různé výpočty interaktivním způsobem, tj. dialogem mezi uživatelem a systémem. Takový způsob práce se může hodit například při řešení různých problémů z oblasti numerické matematiky, zpracování signálů, statistické výpočty apod. V dnešní části se zaměříme na popis použití knihovny Numpy, které se elegantně podařilo spojit dva světy – svět Pythonu s jeho „příjemnou“ a přehlednou syntaxí a svět numerické matematiky a výpočtů s maticemi, který se nejenom z historických důvodů vždy zaměřoval na použití Fortranu a částečně i programovacího jazyka C.
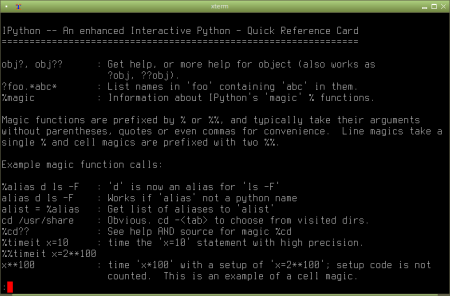
Obrázek 1: IPython je možné ovládat z terminálu (což je základní možnost dostupná ve všech systémech).
Dnes se budeme zabývat především těmi funkcemi a objekty, které jsou dostupné z hlavního balíčku knihovny Numpy. Ve skutečnosti však v této knihovně nalezneme i několik zajímavých a mnohdy velmi užitečných podbalíčků, jejichž jména a stručný popis jsou vypsány v tabulce pod tímto odstavcem:
| Řádek | Jméno podbalíčku | Stručný popis |
|---|---|---|
| 1 | doc | obsahuje dokumentaci ke knihovně i k základním konstrukcím a operacím |
| 2 | lib | základní funkce používané i některými dalšími podbalíčky |
| 3 | random | funkce pro využití generátorů pseudonáhodných číselných hodnot |
| 4 | linalg | funkce z oblasti lineární algebry (bude popsáno příště) |
| 5 | fft | rychlá Fourierova transformace a pomocné funkce (bude popsáno příště) |
| 6 | polynomial | funkce pro práci s polynomy (taktéž bude popsáno příště) |
| 7 | testing | nástroje pro psaní testů |
| 8 | f2py | (jednosměrné) rozhraní mezi Fortranem a Pythonem |
| 9 | distutils | další pomocné nástroje, které přímo nesouvisí s výpočty nad vektory a maticemi, ale se způsobem balíčkování |
Obrázek 2: Alternativně je možné použít textově-grafickou Qt Consoli.
2. Základy, na nichž je postavena knihovna Numpy
Funkce a objekty nabízené knihovnou Numpy se sice volají přímo z Pythonu, ve skutečnosti se však interní datové struktury dosti podstatným způsobem odlišují od datových struktur využívaných samotným Pythonem. V knihovně Numpy tvoří základ datová struktura nazvaná ndarray, která reprezentuje pole o prakticky libovolném počtu dimenzí (ostatně „nd“ ve jménu „ndarray“ značí N-dimensional). Tato pole se liší od běžných seznamů či n-tic v Pythonu, protože ndarray jsou homogenní datovou strukturou: všechny prvky totiž mají shodný typ a navíc všechny prvky leží za sebou, zatímco seznamy v Pythonu jsou měnitelné (prvky lze přidávat a odebírat) a obecně nehomogenní (každý prvek může mít odlišný datový typ). Za tuto velkou flexibilitu se samozřejmě platí, a to jak většími nároky na operační paměť (reference na objekty), tak i pomalejším zpracováním.
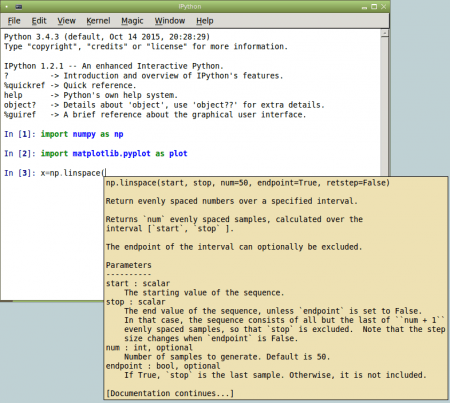
Obrázek 3: Bublinová nápověda je jednou z vylepšení Qt Console oproti klasickému interaktivnímu interpretru.
3. Datové typy prvků, z nichž jsou tvořena pole
Při vytváření polí typu ndarray, ať již se jedná o vektory, matice či o pole s větším množstvím dimenzí, lze specifikovat datový typ všech prvků a dokonce i uspořádání prvků v paměti (buď podle zvyklostí jazyka Fortran nebo jazyka C). Podívejme se nyní na tabulku, v níž jsou vypsány možné typy prvků polí ndarray:
| Řádek | Typ | Formát | Rozsah | Jednoznakový kód |
|---|---|---|---|---|
| 1 | bool | uloženo po bajtech | True/False | '?' |
| 2 | int8 | celočíselný se znaménkem | -128..127 | 'b' |
| 3 | int16 | celočíselný se znaménkem | -32768..32767 | 'h' |
| 4 | int32 | celočíselný se znaménkem | -2147483648..2147483647 | 'i' |
| 5 | int64 | celočíselný se znaménkem | -9223372036854775808..9223372036854775807 | 'l' |
| 6 | uint8 | celočíselný bez znaménka | 0..255 | 'B' |
| 7 | uint16 | celočíselný bez znaménka | 0..65535 | 'H' |
| 8 | uint32 | celočíselný bez znaménka | 0..4294967295 | 'I' |
| 9 | uint64 | celočíselný bez znaménka | 0..18446744073709551615 | 'L' |
| 10 | float16 | plovoucí řádová čárka | poloviční přesnost (half) | 'e' |
| 11 | float32 | plovoucí řádová čárka | jednoduchá přesnost (single) | 'f' |
| 12 | float64 | plovoucí řádová čárka | dvojitá přesnost (double) | 'd' |
| 13 | complex64 | komplexní číslo (dvojice) | 2×float32 | 'F' |
| 14 | complex128 | komplexní číslo (dvojice) | 2×float64 | 'D' |
Poznámka: jednoznakové kódy je možné použít namísto jména typu, viz též funkce popsané v navazujících kapitolách.
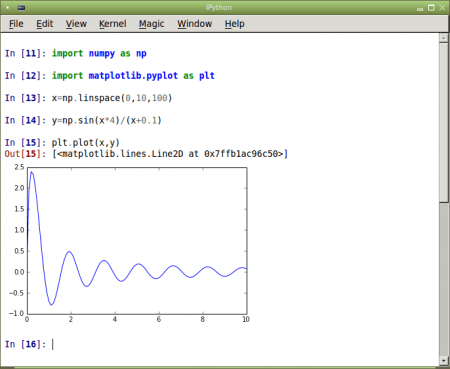
Obrázek 4: Vykreslení funkce s využitím Qt Console.
4. Konstruktory polí
Pole typu ndarray je možné vytvořit několika různými způsoby. Základní funkcí sloužící k převodu různých typů Pythonovských objektů na pole je funkce nazvaná jednoduše numpy.array. Této funkci se předá objekt (což je typicky seznam, n-tice či objekt typu range) a popř. i další nepovinné parametry, které určují typ prvků nově vzniklého pole (dtype), zda se má provést kopie prvků (copy, většinou ano) či způsob uspořádání prvků v poli (order):
array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0)
Obrázek 5: Všechny dnešní demonstrační příklady budeme testovat v IPython Notebooku, jehož prázdný list je zde otevřen ve webovém prohlížeči.
Nepovinný parametr order může nabývat hodnot:
| Order | Význam |
|---|---|
| 'C' | prvky jsou uspořádány jako v jazyku C |
| 'F' | prvky jsou uspořádány jako v jazyku Fortran |
| 'A' | ponecháme na implementaci, který způsob uspořádání zvolit |
Jaký je tedy vlastně rozdíl mezi uspořádáním prvků podle 'C' a 'F'? Předpokládejme matici 3×3 prvky:
| 1 2 3 | | 4 5 6 | | 7 8 9 |
Tato matice může být v paměti uložena následujícím způsobem:
1 2 3 4 5 6 7 8 9 - 'C'
Alternativně je však možné prohodit řádky a sloupce (což více odpovídá matematickému zápisu matice):
1 4 7 2 5 8 3 6 9 - 'F'
Podívejme se nyní na několik praktických použití funkce numpy.array:
# vytvoření pole ze seznamu
numpy.array([1,2,3,4])
array([1, 2, 3, 4])
# vytvoření pole z typu 'range'
numpy.array(range(10))
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# explicitní specifikace typu všech prvků pole
numpy.array(range(10), dtype=numpy.float)
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
# explicitní specifikace uspořádání prvků pole
# (nemá velký význam pro 1D pole=vektory)
numpy.array(range(10), order='C')
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# explicitní specifikace uspořádání prvků pole
# (nemá velký význam pro 1D pole=vektory)
numpy.array(range(10), order='F')
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# vytvoření dvourozměrné matice
numpy.array([[1,2,3],[4,5,6]])
array([[1, 2, 3],
[4, 5, 6]])
Obrázek 6: Nápověda k modulu Numpy.
5. Konstruktor numpy.zeros
Kromě funkce numpy.array se poměrně často setkáme s nutností vytvořit vektor či matici s nulovými prvky. V tomto případě samozřejmě není nutné složitě vytvářet a předávat takové pole do funkce numpy.array, ale lze namísto toho využít funkci nazvanou numpy.zeros, což je rychlejší i méně paměťově náročnější. Té se předá n-tice (musí se skutečně jednat o n-tici, nikoli o seznam parametrů, proto nezapomeňte na závorky) specifikující dimenzi vektoru, matice či N-dimenzionálního pole:
zeros(shape, dtype=float, order='C')
Nepovinný parametr dtype se nastavuje buď na typ nebo na jednoznakový kód uvedený v tabulce ve třetí kapitole.
Podívejme se nyní na způsob použití této funkce:
# jednorozměrný vektor s jediným prvkem
numpy.zeros(1)
array([ 0.])
# jednorozměrný vektor s deseti prvky
numpy.zeros(10)
array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
# matice o velikosti 5x5 prvků, každý prvek je typu float
numpy.zeros((5,5))
array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
# matice o velikosti 5x5 prvků, každý prvek je typu int
numpy.zeros((5,5),dtype=int)
array([[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]])
# použití komplexních čísel
numpy.zeros((2,2),dtype=numpy.complex)
array([[ 0.+0.j, 0.+0.j],
[ 0.+0.j, 0.+0.j]])
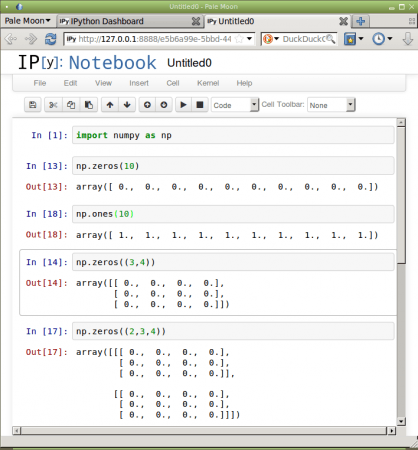
Obrázek 7: Použití funkcí numpy.zeros a numpy.ones.
6. Konstruktor numpy.ones
Dalším velmi často používaným typem vektoru či matice je taková struktura, jejíž všechny prvky mají hodnotu 1. Takový vektor popř. matice je možné vytvořit funkcí numpy.ones
numpy.ones(shape, dtype=None, order='C')
Nepovinný parametr dtype se, podobně jako u předchozí funkce, nastavuje buď na typ nebo na jednoznakový kód uvedený v tabulce ve třetí kapitole.
Opět se podívejme na několik příkladů použití této funkce v praxi:
# jednorozměrný vektor s deseti prvky
numpy.ones(10)
array([ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
# matice se třemi řádky a čtyřmi sloupci
numpy.ones((3,4))
array([[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
# matice se třemi řádky a čtyřmi sloupci
# s explicitní specifikací typu prvků
numpy.ones((3,4), dtype=int)
array([[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]])
# trojrozměrné pole s prvky typu int
numpy.ones((3,4,5), dtype=int)
array([[[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]],
[[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]],
[[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1]]])
# trojrozměrné pole s prvky typu int
# (oproti předchozímu příkladu se velikosti v jednotlivých dimenzích liší)
numpy.ones((5,4,3), dtype=int)
array([[[1, 1, 1],
[1, 1, 1],
[1, 1, 1],
[1, 1, 1]],
[[1, 1, 1],
[1, 1, 1],
[1, 1, 1],
[1, 1, 1]],
[[1, 1, 1],
[1, 1, 1],
[1, 1, 1],
[1, 1, 1]],
[[1, 1, 1],
[1, 1, 1],
[1, 1, 1],
[1, 1, 1]],
[[1, 1, 1],
[1, 1, 1],
[1, 1, 1],
[1, 1, 1]]])
# zde může být použití typu komplexní číslo možná poněkud překvapující,
# ovšem stále platí, že 1=1+0j
numpy.ones((3,2),dtype=numpy.complex)
array([[ 1.+0.j, 1.+0.j],
[ 1.+0.j, 1.+0.j],
[ 1.+0.j, 1.+0.j]])
7. Funkce numpy.arange
Další funkcí určenou pro konstrukci vektoru je numpy.arange, přičemž poněkud zavádějící název „arange“ vznikl složením slov „array“ a „range“. Této funkci se předávají parametry s podobným významem, jaký mají u funkce xrange (Python 2.x) či range (Python 3.x), samozřejmě s tím rozdílem, že návratovou hodnotou funkce numpy.arange se skutečný vektor typu ndarray. Podívejme se na několik možností použití této poměrně nenápadné, ale o to užitečnější funkce:
# při použití jednoho parametru má tento parametr význam hodnoty "stop"
# vytvoří se vektor s prvky od 0 do "stop" (kromě)
numpy.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# specifikace hodnot "start" (včetně) a "stop" (kromě)
numpy.arange(10, 20)
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
# třetí nepovinný parametr určuje krok použitý při generování prvků vektoru
numpy.arange(10, 20, 2)
array([10, 12, 14, 16, 18])
# krok může být samozřejmě záporný
numpy.arange(20, 10, -2)
array([20, 18, 16, 14, 12])
# nemusíme zůstat pouze u celých čísel, protože pracovat je možné i s hodnotami
# typu float a complex
numpy.arange(0,5, 0.1)
array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ,
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1,
2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3,
4.4, 4.5, 4.6, 4.7, 4.8, 4.9])
# použití komplexních konstant
numpy.arange(0+0j, 10+10j, 2+0j)
array([ 0.+0.j, 2.+0.j, 4.+0.j, 6.+0.j, 8.+0.j])
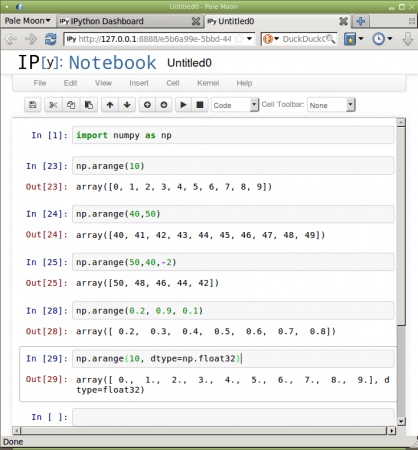
Obrázek 8: Příklady použití funkce numpy.arange v IPython Notebooku.
8. Funkce numpy.linspace
V některých případech nemusí být použití výše popsané funkce numpy.arange tím nejlepším řešením při vytváření vektoru obsahujícího sekvenci číselných hodnot. Typickým příkladem je sekvence generovaná s krokem 0.1, protože hodnotu 0.1 není možné formáty IEEE 754 single ani double přesně reprezentovat. Tím pádem nemusí být z volání funkce numpy.arange ihned zřejmé, kolik prvků se nakonec vygeneruje (typická chyba ±1). Pokud je nutné vytvořit vektor s přesným počtem prvků, může se namísto numpy.arange hodit funkce numpy.linspace, které se předá počáteční hodnota, koncová hodnota a popř. i počet prvků vektoru. Pokud počet prvků není explicitně zadán, použije se hodnota 50. Použití funkce numpy.linspace je tak ve skutečnosti velmi jednoduché:
# pokud se nespecifikuje počet prvků, bude se předpokládat, že výsledný
# vektor má mít padesát prvků
numpy.linspace(0, 1)
array([ 0. , 0.02040816, 0.04081633, 0.06122449, 0.08163265,
0.10204082, 0.12244898, 0.14285714, 0.16326531, 0.18367347,
0.20408163, 0.2244898 , 0.24489796, 0.26530612, 0.28571429,
0.30612245, 0.32653061, 0.34693878, 0.36734694, 0.3877551 ,
0.40816327, 0.42857143, 0.44897959, 0.46938776, 0.48979592,
0.51020408, 0.53061224, 0.55102041, 0.57142857, 0.59183673,
0.6122449 , 0.63265306, 0.65306122, 0.67346939, 0.69387755,
0.71428571, 0.73469388, 0.75510204, 0.7755102 , 0.79591837,
0.81632653, 0.83673469, 0.85714286, 0.87755102, 0.89795918,
0.91836735, 0.93877551, 0.95918367, 0.97959184, 1. ])
# zde explicitně specifikujeme, že výsledný vektor má mít deset prvků
# (tím, že se začíná od nuly, získáme krok 0.11111111...)
numpy.linspace(0, 1, 10)
array([ 0. , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
0.55555556, 0.66666667, 0.77777778, 0.88888889, 1. ])
# zde explicitně specifikujeme, že výsledný vektor má mít jedenáct prvků
numpy.linspace(0, 1, 11)
array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])
# sekvence hodnot samozřejmě může i klesat
numpy.linspace(1, 0, 11)
array([ 1. , 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0. ])
# použít je možné i komplexní čísla
numpy.linspace(0+0j, 1+0j, 10)
array([ 0.00000000+0.j, 0.11111111+0.j, 0.22222222+0.j, 0.33333333+0.j,
0.44444444+0.j, 0.55555556+0.j, 0.66666667+0.j, 0.77777778+0.j,
0.88888889+0.j, 1.00000000+0.j])
# použít je možné i komplexní čísla
numpy.linspace(0+0j, 0+1j, 10)
array([ 0.+0.j , 0.+0.11111111j, 0.+0.22222222j, 0.+0.33333333j,
0.+0.44444444j, 0.+0.55555556j, 0.+0.66666667j, 0.+0.77777778j,
0.+0.88888889j, 0.+1.j ])
# další možnost použití komplexních čísel
numpy.linspace(0+0j, 1+1j, 10)
array([ 0.00000000+0.j , 0.11111111+0.11111111j,
0.22222222+0.22222222j, 0.33333333+0.33333333j,
0.44444444+0.44444444j, 0.55555556+0.55555556j,
0.66666667+0.66666667j, 0.77777778+0.77777778j,
0.88888889+0.88888889j, 1.00000000+1.j ])
Obrázek 9: Příklady použití funkce numpy.linspace v IPython Notebooku.
9. Přetypování všech prvků v poli
Při práci s rozměrnými maticemi je v některých případech nutné provést přetypování všech prvků matice (či vektoru). Tuto operaci je možné provést dvěma způsoby. První způsob spočívá v tom, že se názvy datových typů, jako je například numpy.float32, numpy.int32 či numpy.complex128 (viz též tabulku uvedenou ve třetí kapitole), přímo použijí jako funkce pro přetypování:
# změna typu
numpy.float32(1.0)
# přetypování
numpy.int64([1,2,3,4])
# přetypování
numpy.float16([1,2,3,4])
array([ 1., 2., 3., 4.], dtype=float16)
# vektor čísel typu float
numpy.linspace(0, 1, 10)
array([ 0. , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
0.55555556, 0.66666667, 0.77777778, 0.88888889, 1. ])
# přetypování na vektor celých čísel
numpy.int32(numpy.linspace(0, 1, 10))
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 1], dtype=int32)
Alternativně se používá metoda (nikoli funkce) nazvaná astype, která se volá pro daný vektor, matici, či obecné n-dimenzionální pole. Této metodě se předá požadovaný typ prvků výsledného pole:
pole.astype(numpy.float32)
pole.astype(numpy.int8)
pole.astype(numpy.complex64)
a=numpy.arange(0, 10)
a.astype(numpy.complex64)
array([ 0.+0.j, 1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j, 5.+0.j, 6.+0.j,
7.+0.j, 8.+0.j, 9.+0.j], dtype=complex64)
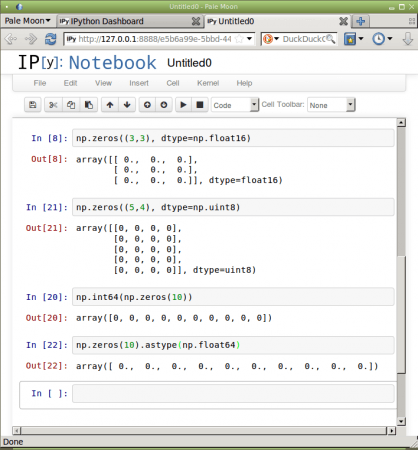
Obrázek 10: Příklady přetypování a použití metody astype v IPython Notebooku.
10. Zjištění tvaru pole pomocí funkce numpy.shape
Termínem „tvar pole“ je v knihovně Numpy myšlena n-tice obsahující rozměry pole v jednotlivých dimenzích. Pro vektor tato n-tice obsahuje jediné číslo s délkou vektoru, pro matici obsahuje n-tice dvě čísla s počtem řádků a sloupců atd. Zjištění tvaru libovolného pole je tedy značně jednoduché:
# jednorozměrný vektor
a=numpy.array([1,2,3])
# dvourozměrná matice
b=numpy.array([[1,2,3],[4,5,6]])
# tvar vektoru
a.shape
(3,)
# tvar matice
b.shape
(2, 3)
# trojrozměrné pole
c=numpy.zeros((2,3,4))
c
array([[[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]],
[[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.],
[ 0., 0., 0., 0.]]])
# tvar trojrozměrného pole
c.shape
(2, 3, 4)
# další trojrozměrné pole, tentokrát vytvořené explicitně
d=numpy.array([[[1,2], [3,4]], [[5,6], [7,8]]])
numpy.shape(d)
(2, 2, 2)
11. Změna tvarů polí s využitím funkce numpy.reshape
Další velmi důležitou funkcí, s níž se v praxi často setkáme, je funkce nazvaná numpy.reshape, která dokáže změnit velikost matice a vhodným způsobem přeorganizovat prvky v původní matici. Této funkci se předávají dva parametry – prvním parametrem je vstupní pole (vektor, matice, ...), druhým parametrem pak specifikace tvaru výsledného pole, přičemž tvar je reprezentován n-ticí, v níž jsou uloženy velikosti pole v jednotlivých dimenzích. Podívejme se na několik příkladů:
# běžná matice se dvěma řádky a třemi sloupci
b=numpy.array([[1,2,3],[4,5,6]])
# změna tvaru matice na 3x2 prvky
numpy.reshape(b,(3,2))
array([[1, 2],
[3, 4],
[5, 6]])
# zde vlastně dostaneme původní matici
numpy.reshape(b,(2,3))
array([[1, 2, 3],
[4, 5, 6]])
# vytvoření matice s jediným řádkem
numpy.reshape(b,(1,6))
array([[1, 2, 3, 4, 5, 6]])
# vytvoření matice s jediným sloupcem
numpy.reshape(b,(6,1))
array([[1],
[2],
[3],
[4],
[5],
[6]])
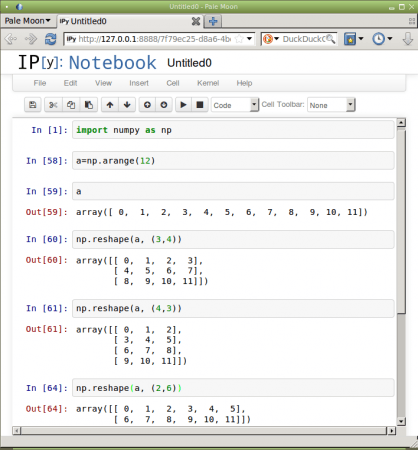
Obrázek 11: Příklady použití funkce numpy.reshape na dvanáctiprvkový vstupní vektor v IPython Notebooku.
Při použití funkce numpy.reshape si dejte pozor na to, aby se při změně tvarů pole přesně dodržel počet prvků. Pokud by se měl počet prvků změnit, dojde ke vzniku výjimky:
a=numpy.array([1,2,3])
numpy.reshape(a, (2,2))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-74-fa31403e23c0> in <module>()
----> 1 numpy.reshape(a,(2,2))
/usr/lib/python3/dist-packages/numpy/core/fromnumeric.py in reshape(a, newshape, order)
216 except AttributeError:
217 return _wrapit(a, 'reshape', newshape, order=order)
--> 218 return reshape(newshape, order=order)
219
220
ValueError: total size of new array must be unchanged
K chybě dojde i v opačném případě, tj. pokud by byl počet prvků vstupního pole sice dostatečný, ale některé prvky by ve výsledném (vytvářeném) poli přebývaly:
x=numpy.arange(0,12)
numpy.reshape(x, (2,2))
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-47-0943fdd71a8f> in <module>()
----> 1 numpy.reshape(x, (2,2))
/usr/lib/python3/dist-packages/numpy/core/fromnumeric.py in reshape(a, newshape, order)
216 except AttributeError:
217 return _wrapit(a, 'reshape', newshape, order=order)
--> 218 return reshape(newshape, order=order)
219
220
ValueError: total size of new array must be unchanged
Proč tomu tak je? Ve skutečnosti se totiž funkcí numpy.reshape nevytváří zcela nové pole s jiným tvarem, ale dochází pouze ke vzniku odlišného pohledu na jediné (zdrojové) pole.
Další příklad pro vstupní vektor s 24 prvky a výsledná pole se třemi či čtyřmi dimenzemi:
# zdrojový vektor
m=numpy.arange(24)
m
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
# změna tvaru na trojrozměrné pole
numpy.reshape(m, (2,3,4))
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
# změna tvaru vektoru na trojrozměrné pole
numpy.reshape(m, (4,2,3))
array([[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]],
[[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23]]])
# změna tvaru vektoru na čtyřrozměrné pole
numpy.reshape(m, (2,2,2,3))
array([[[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]]],
[[[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23]]]])
# změna tvaru vektoru na čtyřrozměrné pole
numpy.reshape(m, (3,2,2,2))
array([[[[ 0, 1],
[ 2, 3]],
[[ 4, 5],
[ 6, 7]]],
[[[ 8, 9],
[10, 11]],
[[12, 13],
[14, 15]]],
[[[16, 17],
[18, 19]],
[[20, 21],
[22, 23]]]])
12. Vliv nepovinného parametru „order“ na (zdánlivou) změnu tvaru pole
S nepovinným parametrem „order“ jsme se již setkali u funkce numpy.array. Tento parametr lze použít i při změně tvaru pole funkcí numpy.reshape. Opět platí, že je možné specifikovat řazení prvků podle jazyka Fortran či podle jazyka C. Změní se tedy pohled na původní pole resp. pohled na to, jakým způsobem knihovna Numpy počítá indexy prvků (k vlastnímu přeorganizování pole v operační paměti však nedojde):
# nyní vyzkoušíme význam nepovinného parametru order
numpy.reshape(m, (6,4))
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
numpy.reshape(m, (6,4), order='C')
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
numpy.reshape(m, (6,4), order='F')
array([[ 0, 6, 12, 18],
[ 1, 7, 13, 19],
[ 2, 8, 14, 20],
[ 3, 9, 15, 21],
[ 4, 10, 16, 22],
[ 5, 11, 17, 23]])
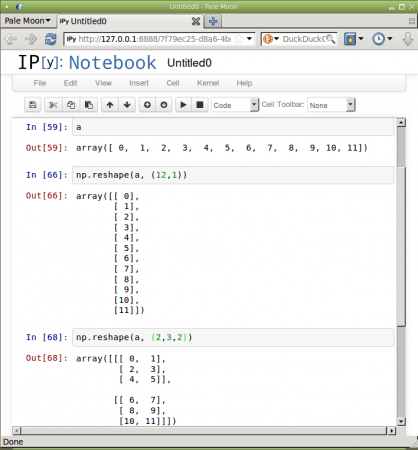
Obrázek 12: Příklady použití funkce numpy.reshape na dvanáctiprvkový vstupní vektor v IPython Notebooku.
13. Předchozí části seriálu
- Vývojová prostředí ve Fedoře (1. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-1-dil/ - Vývojová prostředí ve Fedoře (2. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-2-dil/ - Vývojová prostředí ve Fedoře (3. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-3-dil/ - Vývojová prostředí ve Fedoře (4. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-4-dil/ - Integrovaná vývojová prostředí ve Fedoře: PyDev
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Integrovaná vývojová prostředí ve Fedoře: PyDev (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: IPython a IPython Notebook
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-ipython-a-ipython-notebook/
14. Odkazy na Internetu
- IPython homepage
http://ipython.org/ - Dokumentace k IPythonu
http://ipython.org/documentation.html# - IPython Tutorial
http://ipython.readthedocs.org/en/stable/interactive/tutorial.html - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb - 0MQ Home Page
http://zeromq.org/ - Is IPython Notebook ever used as an IDE, or merely for presentations?
https://www.reddit.com/r/IPython/comments/1uk7hp/is_ipython_notebook_ever_used_as_an_ide_or_merely/ - The IDE as a Bad Programming Language Enabler
https://dzone.com/articles/ide-bad-programming-language - Enhanced Interactive Python with IPython
http://www.onlamp.com/pub/a/python/2005/01/27/ipython.html - Direct mode
https://en.wikipedia.org/wiki/Direct_mode - Seznámení s Python IDE Spyder (článek vyšel zde na mojefedora.cz)
http://mojefedora.cz/seznameni-s-python-ide-spyder/ - Stránka s popisem různých IDE pro Python
http://quintagroup.com/cms/python/ide - Eclipse (stránka o frameworku na Fedoraproject.org)
https://fedoraproject.org/wiki/Eclipse - PyDev (hlavní stránka)
http://pydev.sourceforge.net/index.html - PyDev (download, v podstatě není zapotřebí)
http://pydev.sourceforge.net/download.html - PyDev (stránka s metainformacemi o PyDev pluginu, použita v Eclipse)
http://www.pydev.org/updates/ - PyDev (stránka s pluginem, použita v Eclipse)
https://dl.bintray.com/fabioz/pydev/4.5.4/ - Certifikát, který lze do Eclipse doinstalovat
http://www.pydev.org/pydev_certificate.cer - PyDev FAQ
http://pydev.sourceforge.net/faq.html - PyDev (Wikipedia)
https://en.wikipedia.org/wiki/PyDev - Python (oficiální stránky projektu)
https://www.python.org/ - Jython
http://www.jython.org/ - IronPython
http://ironpython.net/ - Python 3.5.1 documentation
https://docs.python.org/3/ - PyDev: Unittest integration
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Continuous unit testing with Pydev (Python and Eclipse)
http://stackoverflow.com/questions/1015581/continuous-unit-testing-with-pydev-python-and-eclipse - Test-driven development
https://en.wikipedia.org/wiki/Test-driven_development


