Knihovna Numpy, s níž jsme se seznámili v předchozích článcích, nabízí uživatelům poměrně velké množství modulů a funkcí vhodných pro zpracování numerických dat, včetně poměrně pokročilých operací typu FFT (rychlá Fourierova transformace), řešení soustavy lineárních rovnic apod. Ovšem naplno tuto knihovnu využijeme teprve až ve chvíli, kdy ji propojíme s další knihovnou, která se jmenuje matplotlib. Knihovna matplotlib totiž umožňuje vytvářet a modifikovat různé typy grafů, a to mnohdy velmi jednoduchým a přímočarým způsobem.
Obsah
2. Vykreslení průběhu funkce sinus
4. Vykreslení průběhů dvou funkcí do jediného grafu
5. Změna stylu vykreslování a přidání legendy
7. Kombinace různých stylů vykreslování grafů
8. Zobrazení mřížky a nastavení rozsahů na obou osách
11. Vykreslení průběhů většího množství funkcí v polárním grafu
12. Vyplnění plochy pod funkcí v polárním grafu
1. Integrovaná vývojová prostředí ve Fedoře: vykreslování grafů s využitím knihoven Numpy a matplotlib
V předchozích dvou částech [1], [2] seriálu o vývojových prostředích, která jsou dostupná všem programátorům využívajícím distribuci Fedora, jsme si vysvětlili některé koncepty, na nichž je postavena knihovna Numpy. V mnoha případech se však nespokojíme pouze s výstupem výpočtů ve formě různých tabulek, ale potřebujeme vytvořit i vhodný grafický výstup, tj. nějaký graf či diagram. Podporu pro vykreslování grafů sice přímo v knihovně Numpy nenalezneme (což je ostatně naprosto v pořádku, neboť její zaměření je poněkud odlišné), ovšem Numpy je možné velmi snadno propojit s knihovnou matplotlib, která je na práci s různými typy grafů určená.
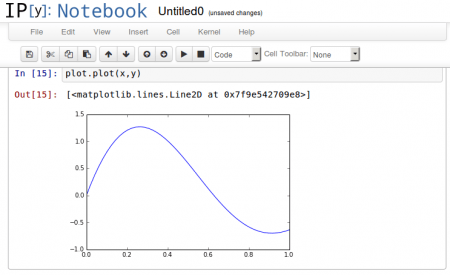
Obrázek 1: Knihovnu matplotlib je možné použít i interaktivně v IPythonu či v IPython Notebooku.
Právě vzájemnou kombinací obou knihoven Numpy+matplotlib lze relativně snadno dosáhnout velmi pěkných výsledků plně porovnatelných s výsledky vytvořenými komerčními balíky. V dnešním článku se seznámíme pouze se základy práce s knihovnou matplotlib. Nejprve si ukážeme tvorbu klasických grafů funkcí jedné proměnné, následně do grafu přidáme průběh další funkce, popisky os, legendu, popisky vlastních průběhů atd. V závěru si pak ukážeme další typy grafů, zejména polární grafy. V navazující části si pak ukážeme tvorbu grafů s konturami, 3D grafů funkcí se dvěma nezávislými proměnnými, 3D grafů funkcí typu x,y=f(t), x,y,z=f(t) apod. Přesvědčíme se, že možnosti knihovny matplotlib jsou skutečně široké a přitom je její použití poměrně jednoduché a snadno pochopitelné (pokud samozřejmě vynecháme některé pokročilejší operace).
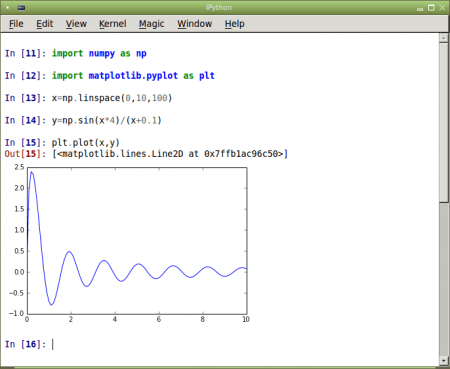
Obrázek 2: Vykreslení průběhu funkce s využitím pouhých pěti příkazů (z toho dva příkazy slouží k importu knihoven).
2. Vykreslení průběhu funkce sinus
Popišme si velmi jednoduchý demonstrační příklad (naprogramovaný v Pythonu 3), který po svém spuštění vykreslí graf s průběhem funkce sinus. V příkladu nalezneme pouze osm programových řádků. Nejprve je nutné naimportovat hlavní modul knihovny Numpy nazvaný numpy a následně i submodul plt z knihovny matplotlib. Většina aplikací, ale i demonstračních příkladů, s nimiž se setkáte, používá pro importované moduly zkratky np a plt, čehož se z důvodu zachování konzistence budeme držet i my. Následně je pomocí funkce numpy.linspace() (tu již dobře známe z předchozích dvou článků) vytvořeno pole sta prvků s hodnotami od 0 do 2π. Na toto pole je aplikována funkce numpy.sin(), jejímž výsledkem je nové stoprvkové pole (hodnoty prvků leží v rozsahu od -1 do 1). Funkcí matplotlib.pyplot.plot() je vykreslen průběh funkce, ovšem graf ještě není zobrazen, takže do něj můžeme přidat popis obou os a graf následně zobrazit příkazem matplotlib.pyplot.show(). Způsob zobrazení závisí na nastavení Pythonu; implicitně se použije speciální prohlížeč naprogramovaný s použitím knihovny Tk:
# Knihovny Numpy a matplotlib
#
# První demonstrační příklad:
# - vykreslení průběhu funkce sin
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose
y = np.sin(x)
# vykreslit průběh funkce
plt.plot(x, y)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x)")
# zobrazení grafu
plt.show()
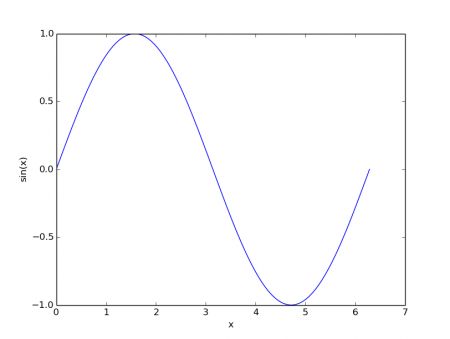
Obrázek 3: Průběh funkce sin(x) vykreslený prvním demonstračním příkladem.
3. Volba výstupního souboru
Implicitní prohlížeč, o němž jsme se zmínili v předchozí kapitole, sice dokáže uložit nakreslený graf do výstupního souboru, ovšem mnohdy je nutné, aby knihovna matplotlib graf vyexportovala automaticky (programově). Můžeme si například představit generátor výsledků spouštěný ze skriptu, pomocnou službu pro tvorbu grafů umisťovaných na webové stránky apod. Při takovýchto požadavcích, které jsou poměrně časté, je možné využít funkce matplotlib.pyplot.savefig(), které se v nejjednodušším případě předá pouze jméno výstupního souboru. Tato funkce pak na základě analýzy přípony souboru rozhodne o tom, který formát použije. K dispozici jsou mj. tyto formáty:
| # | Koncovka | Formát |
|---|---|---|
| 1 | png | rastrový formát PNG |
| 2 | dokument ve formátu PDF s vektorovým grafem | |
| 3 | eps | vektorový formát Encapsulated PostScript (varianta PostScriptu určená pro vložení do dalších dokumentů, včetně (La)TeXu) |
| 4 | ps | vektorový formát PostScript |
| 5 | svg | vektorový formát SVG |
Použití funkce matplotlib.pyplot.savefig() je v praxi velmi snadné, o čemž se ostatně můžete sami přesvědčit po porovnání zdrojového kódu prvního demonstračního příkladu a příkladu druhého, do něhož jsme pouze vložili vytvoření pěti souborů s exportovaným grafem:
# Knihovny Numpy a matplotlib
#
# Druhý demonstrační příklad:
# - vykreslení průběhu funkce sin
# - uložení grafu do různých typů souboru
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose
y = np.sin(x)
# vykreslit průběh funkce
plt.plot(x, y)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x)")
# vykreslení a uložení grafu do různých typů souborů
plt.savefig("example02.png")
plt.savefig("example02.pdf")
plt.savefig("example02.eps")
plt.savefig("example02.ps")
plt.savefig("example02.svg")
# zobrazení grafu
plt.show()
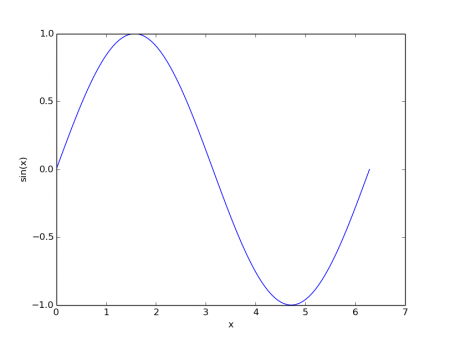
Obrázek 4: Průběh funkce sin(x) vykreslený druhým demonstračním příkladem.
4. Vykreslení průběhů dvou funkcí do jediného grafu
Velmi často se můžeme setkat s požadavkem vložení průběhů několika funkcí do jediného grafu. Zde knihovna matplotlib svým uživatelům nabízí větší množství řešení. Je například možné do jednoho obrázku či dokumentu vložit více grafů s totožnou x-ovou osou (a většinou odlišným měřítkem na y-ových osách), popř. lze skutečně sloučit větší množství průběhů v jediném grafu. Ukažme si nejdříve druhou zmiňovanou možnost, tj. vytvoření grafu s dvěma funkcemi, ovšem s totožnými x-ovými a y-ovými osami. I u takto vytvořeného grafu můžeme použít již zmíněnou funkci matplotlib.pyplot.plot(), které se ovšem předají čtyři pole: hodnoty na ose x, hodnoty první funkce, opět hodnoty na ose x (pro nás stejné pole) a hodnoty druhé funkce. Žádné další operace nejsou zapotřebí, což je ostatně patrné i při pohledu na zdrojový kód dnešního třetího demonstračního příkladu:
# Knihovny Numpy a matplotlib
#
# Třetí demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos
# do jediného grafu
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
# vykreslit průběh obou funkcí
plt.plot(x, y1, x, y2)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
# zobrazení grafu
plt.show()
Poznámka: toto řešení není příliš vhodné v situaci, kdy jsou hodnoty obou funkcí značně rozdílné, neboť se používá stejné měřítko.
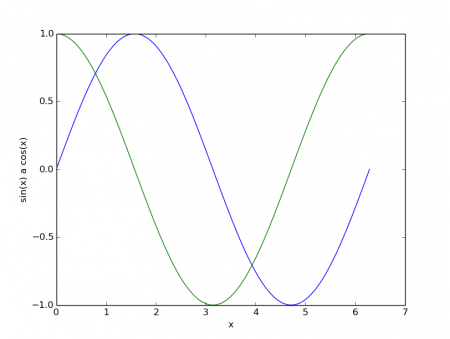
Obrázek 5: Graf, na němž jsou nakresleny průběhy dvou funkcí.
5. Změna stylu vykreslování a přidání legendy
Při pohledu na graf vykreslený na obrázku číslo 5 je patrné, že knihovna matplotlib automaticky zvolila pro průběh každé funkce odlišnou barvu, ovšem styl vykreslení (šířka čáry atd.) zůstal stejný. Pokud budeme potřebovat ovlivnit styl vykreslování průběhů funkcí, lze to samozřejmě zařídit a to poměrně jednoduše. Funkci matplotlib.pyplot.plot() je totiž možné předat nepovinný (a nepojmenovaný) parametr typu řetězec, v němž je „zakódována“ jak barva (první písmeno anglického názvu barvy), tak i styl vykreslování (-- je plná čára, - čárkovaná čára, . tečkovaná čára apod.). Dalším nepovinným parametrem, tentokrát již pojmenovaným, je parametr „label“, pomocí něhož je možné libovolný průběh funkce označit jménem. Toto jméno se následně použije například v legendě přidané do grafu funkcí matplotlib.pyplot.legend(). Nepovinným pojmenovaným parametrem loc se popíše, do kterého místa grafu se má legenda vložit:
# Knihovny Numpy a matplotlib
#
# Čtvrtý demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos a sinc
# do jediného grafu
# - změna stylu vykreslování průběhů funkcí
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0.01, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
# hodnoty na y-ové ose: třetí funkce
y3 = np.sin(x)/x
# vykreslit průběh všech tří funkcí
# se změnou stylu vykreslování
plt.plot(x, y1, "b-", label="sin")
plt.plot(x, y2, "r.", label="cos")
plt.plot(x, y3, "g--", label="sinc")
# přidání legendy
plt.legend(loc="lower left")
# popis os
plt.xlabel("x")
plt.ylabel("sin(x), cos(x) a sinc(x)")
# zobrazení grafu
plt.show()
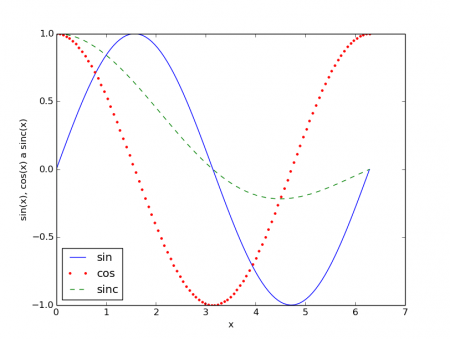
Obrázek 6: Různé styly vykreslování. Povšimněte si, že v grafu je v levém dolním rohu zobrazena i legenda.
6. Vyplnění plochy pod funkcí
V případě, že se namísto funkce matplotlib.pyplot.plot() použije pro vykreslení grafu funkce pojmenovaná matplotlib.pyplot.fill(), změní se poměrně zásadním způsobem styl vykreslení. Namísto (lomené) čáry se totiž plocha pod funkcí vyplní konstantní barvou. Tu je možné zadat slovně, například "red", "yellow" atd. Ovšem ve chvíli, kdy se funkce překrývají, by dříve vykreslený průběh nebyl viditelný, protože by jedna barevná plocha překreslila plochu druhou. Abychom tomuto problému předešli, stačí knihovně matplotlib předepsat průhlednost barvy v rozsahu 0.0 až 1.0. Konkrétně to znamená, že při požadavku na vykreslení dvou funkcí a použití barev s průhledností 30% můžeme zadat příkaz plt.fill(x, y1, "red", x, y2, "yellow", alpha=0.3). Podívejme se na úplné znění zdrojového kódu dnešního pátého demonstračního příkladu, v němž je tento příkaz použit:
# Knihovny Numpy a matplotlib
#
# Pátý demonstrační příklad:
# - vykreslení průběhů funkcí sin a sinc
# do jediného grafu
# s vyplněním plochy pod průběhu
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.sin(3*x)/(x+1)
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.fill(x, y1, "red", x, y2, "yellow", alpha=0.3)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a sinc(3x)")
# zobrazení grafu
plt.show()
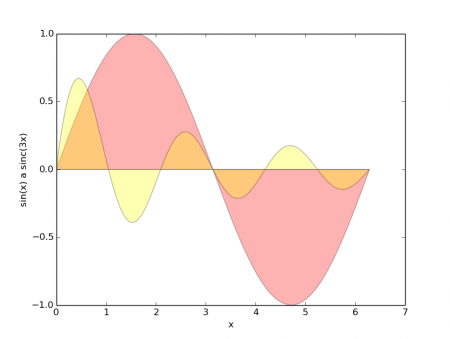
Obrázek 7: Dva průběhy funkcí vykreslených červenou a žlutou barvou s průhledností 30%.
7. Kombinace různých stylů vykreslování grafů
V knihovně matplotlib je možné jednotlivé příkazy pro vykreslení funkcí vzájemně kombinovat. V dnešním šestém demonstračním příkladu je vykreslena funkce sinus, dále pak známá funkce sinc (s posunutou osou) a následně dva průběhy funkcí, které vlastně tvoří obálku sinc. Funkce sinus i sinc jsou vykresleny takovým způsobem, že je plocha pod průběhem funkce vyplněna, zatímco obálky jsou pouze naznačeny čárkovanými čarami. Legenda se navíc přesunula do pravého horního rohu, kde je pro ni mnohem více místa:
# Knihovny Numpy a matplotlib
#
# Šestý demonstrační příklad:
# - vykreslení průběhů čtyř různých funkcí
# do jediného grafu
# s vyplněním plochy pod průběhu
# - kombinace různých stylů vykreslení
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0.001, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(5*x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.sin(5*x)/(x+1/2)
# hodnoty na y-ové ose: třetí čtvrtá funkce
y3 = 1/(x+1/2)
y4 = -y3
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.fill(x, y1, "yellow", alpha=0.3, label="sin x")
plt.fill(x, y2, "r.", alpha=1.0, label="sinc 5x")
plt.plot(x, y3, "g--", label="obalka sinc")
plt.plot(x, y4, "g--", label="obalka sinc")
# přidání legendy
plt.legend(loc="upper right")
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a sinc(3x)")
# zobrazení grafu
plt.show()
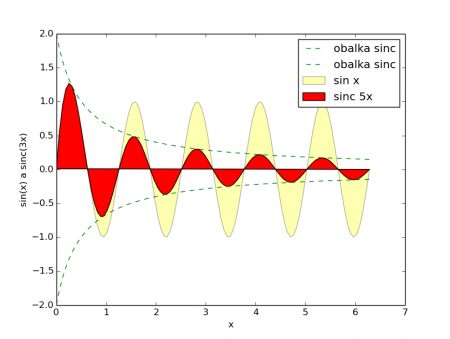
Obrázek 8: Kombinace několika různých stylů vykreslení funkcí.
8. Zobrazení mřížky a nastavení rozsahů na obou osách
Doposud nakreslené grafy ve skutečnosti nevypadaly příliš profesionálně, a to mj. i proto, že bylo poměrně obtížné rozeznat počátek souřadnic atd. Poměrně snadno je možné tento nedostatek opravit přidáním mřížky příkazem matplotlib.pyplot.grid(True). Navíc ještě můžeme zvětšit oblast grafu pomocí matplotlib.pyplot.axis([-1, 8, -1.5, 1.5]), kde čtveřice čísel značí postupně xmin, xmax, ymin a ymax (přesněji řečeno se nezvětší samotný obrázek s grafem, ale dojde ke změně jeho měřítka). Vlastní průběh funkce tedy přestane zasahovat do samotných hranic grafu, takže nový výsledek vypadá mnohem lépe:
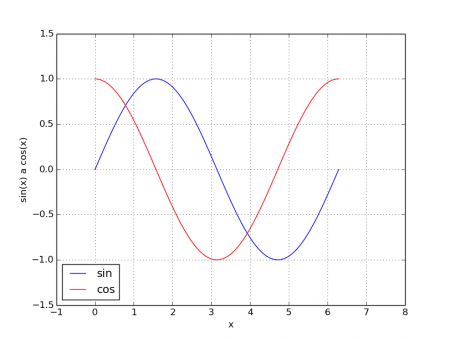
Obrázek 9: Graf se zobrazením mřížky a změnou měřítka (plochy).
Podívejme se na upravený zdrojový kód:
# Knihovny Numpy a matplotlib
#
# Sedmý demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos
# - nastavení mřížky
# - nastavení rozsahů na obou osách
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.plot(x, y1, "b-", label="sin")
plt.plot(x, y2, "r-", label="cos")
# přidání legendy
plt.legend(loc="lower left")
# nastavení rozsahů na obou osách
plt.axis([-1, 8, -1.5, 1.5])
# povolení zobrazení mřížky
plt.grid(True)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
# zobrazení grafu
plt.show()
9. Přidání popisků do grafů
Nyní se již dostáváme k poněkud složitějšímu úkolu. Předpokládejme, že je do grafu se dvěma funkcemi zapotřebí přidat popisky se šipkami ukazujícími na určité místo na křivce. Výsledek by měl vypadat nějak takto:
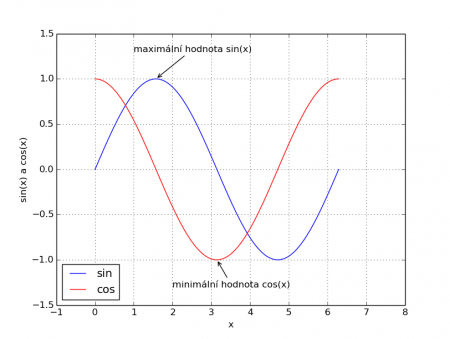
Obrázek 10: Přidání popisků do grafů.
Průběhy obou funkcí si necháme vykreslit nám již známým způsobem, zde tedy k žádné podstatné změně nedojde. Ovšem pro přidání popisků již musíme použít novou funkci, konkrétně funkci pojmenovanou matplotlib.pyplot.annotate(). Této funkci se předá jeden nepojmenovaný parametr s popiskem, tj. například "maximální hodnota sin(x)". Dále budou následovat pojmenované parametry, konkrétně parametr se jménem xy a přesnou souřadnicí vrcholu šipky (tj. místa, kam šipka míří), dále pak parametr se jménem xytext, jehož hodnotou je souřadnice umístění textu (n-tice) a posledním parametrem je parametr s názvem arrowprops (properties), přes nějž nastavíme styl vykreslené šipky:
plt.annotate("maximální hodnota sin(x)",
xy=(np.pi/2,1.0),
xytext=(1, 1.3),
arrowprops=dict(arrowstyle="->"))
Do grafu ve skutečnosti vložíme dva popisky, což je ostatně patrné z výpisu zdrojového kódu osmého demonstračního příkladu:
# Knihovny Numpy a matplotlib
#
# Osmý demonstrační příklad:
# - vykreslení průběhů funkcí sin a cos
# - nastavení mřížky
# - nastavení rozsahů na obou osách
# - přidání popisku přímo do grafu
import numpy as np
import matplotlib.pyplot as plt
# hodnoty na x-ové ose
x = np.linspace(0, 2*np.pi, 100)
# hodnoty na y-ové ose: první funkce
y1 = np.sin(x)
# hodnoty na y-ové ose: druhá funkce
y2 = np.cos(x)
# vykreslit průběh obou funkcí
# se změnou stylu vykreslování
plt.plot(x, y1, "b-", label="sin")
plt.plot(x, y2, "r-", label="cos")
# přidání legendy
plt.legend(loc="lower left")
# nastavení rozsahů na obou osách
plt.axis([-1, 8, -1.5, 1.5])
# povolení zobrazení mřížky
plt.grid(True)
# popis os
plt.xlabel("x")
plt.ylabel("sin(x) a cos(x)")
# vložit první popisek do grafu
plt.annotate("maximální hodnota sin(x)",
xy=(np.pi/2,1.0),
xytext=(1, 1.3),
arrowprops=dict(arrowstyle="->"))
# vložit druhý popisek do grafu
plt.annotate("minimální hodnota cos(x)",
xy=(np.pi,-1.0),
xytext=(2,-1.3),
arrowprops=dict(arrowstyle="->"))
# zobrazení grafu
plt.show()
10. Základní polární graf
Pokud je zapotřebí vykreslit polární graf, je možné postupovat následujícím způsobem. Nejprve se plocha obrázku či dokumentu určená pro vykreslení grafu rozdělí do pomyslné mřížky o velikosti 1×1 buňka. Do této mřížky se funkcí matplotlib.pyplot.subplot() vloží „podgraf“, u něhož se pojmenovaným parametrem projection specifikuje použitá projekce. Magická konstanta 111 při volání této funkce značí, že se skutečně má vytvořit mřížka 1×1 buňka a podgraf se má vložit do této buňky (ta má index 1). Další vykreslování již vlastně známe, ovšem s tím nepatrným rozdílem, že se nevolá funkce matplotlib.pyplot.plot(), ale metoda objektu získaného výše zmíněnou funkcí matplotlib.pyplot.subplot(). Dále si povšimněte toho, že namísto polí pojmenovaných x a y používáme pole hodnot se jmény theta a radius, což se pro tento typ grafu hodí mnohem více:
# Knihovny Numpy a matplotlib # # Devátý demonstrační příklad: # - základní polární graf import numpy as np import matplotlib.pyplot as plt # úhel v polárním grafu theta = np.linspace(0.01, 2*np.pi, 150) # vzdálenost od středu radius = np.log(theta) ax=plt.subplot(111, projection="polar") # vykreslit průběh funkce # v polárním grafu ax.plot(theta, radius) # zobrazení grafu plt.show()
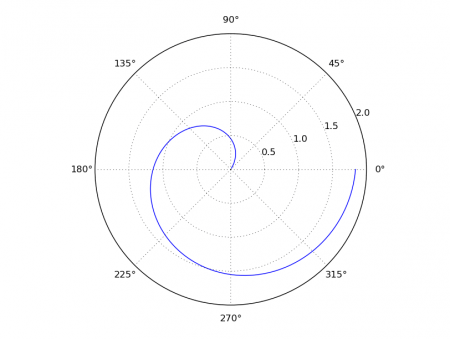
Obrázek 11: Polární graf se slavnou logaritmickou spirálou.
11. Vykreslení průběhů většího množství funkcí v polárním grafu
Podobně, jako tomu bylo u normálního grafu se dvěma na sebe kolmými osami, i v polárním grafu je možné současně zobrazit větší množství průběhů funkcí; postačuje pouze volat několikrát metodu plot objektu získaného voláním funkce matplotlib.pyplot.subplot(). Taktéž je možné specifikovat styl zobrazení průběhu jednotlivých funkcí, pojmenovat daný průběh (resp. přesněji řečeno mu přiřadit jméno) apod. V dnešním předposledním demonstračním příkladu jsou v polárním grafu zobrazeny průběhy tří funkcí – dvě funkce vytvoří spirálu (první je lineární, druhá pak logaritmická), třetí funkce má v polárním grafu tvar srdce. Podívejme se na zdrojový kód tohoto příkladu:
# Knihovny Numpy a matplotlib # # Desátý demonstrační příklad: # - vykreslení průběhů několika funkcí # - do polárního grafu import numpy as np import matplotlib.pyplot as plt # úhel v polárním grafu theta = np.linspace(0.01, 2*np.pi, 150) # první funkce: vzdálenost od středu radius1 = theta # druhá funkce: vzdálenost od středu radius2 = 2*np.abs(theta-np.pi) # třetí funkce: vzdálenost od středu radius3 = 2*np.log(theta) ax=plt.subplot(111, projection="polar") # vykreslit průběh první funkce # v polárním grafu ax.plot(theta, radius1, "r.", label="f1") # vykreslit průběh druhé funkce # v polárním grafu ax.plot(theta, radius2, "g", label="f2") # vykreslit průběh třetí funkce # v polárním grafu ax.plot(theta, radius3, "b--", label="f3") # přidání legendy plt.legend(loc="lower left") # zobrazení grafu plt.show()
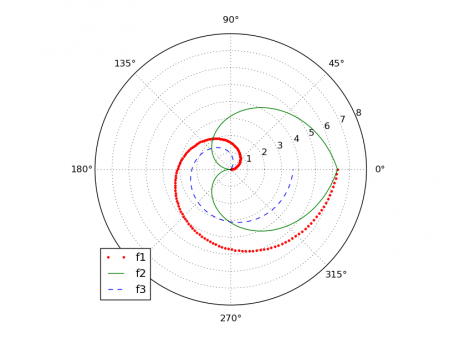
Obrázek 12: Kombinované zobrazení několika funkcí v jediném polárním grafu.
12. Vyplnění plochy pod funkcí v polárním grafu
I funkce, jejichž průběh má být vykreslen v polárním grafu, mohou být pod svou křivkou vyplněny, postačuje pouze namísto metody nazvané plot() zavolat metodu pojmenovanou fill(). Většinou je navíc nutné u vyplněného průběhu funkce specifikovat kromě barvy i průhlednost vykreslované plochy (v našem případě bude nastavena na 30%). V dnešním jedenáctém a současně i posledním demonstračním příkladu jsou vykresleny dvě funkce, jedna s použitím metody plot(), druhá pak pomocí fill(). Navíc si povšimněte další zajímavé vlastnosti – pole theta obsahující úhly je naplněno prvky s hodnotami od 0 až do 4π. Co to znamená v praxi? – z pohledu na obrázek s grafem je patrné, že jsou zobrazeny dvě celé otočky spirály, protože 4π rad odpovídá 720°:
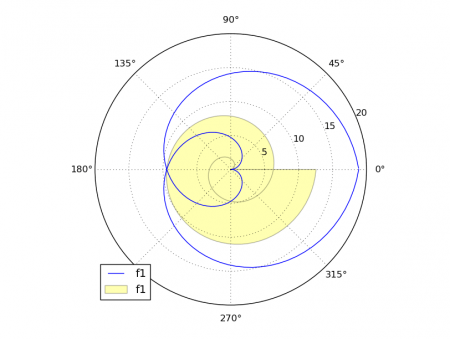
Obrázek 13: Spirála je vykreslena tak, že se plocha pod křivkou vyplnila. Povšimněte si, že v grafu došlo k dvěma úplným otočkám spirály.
Následuje úplný kód tohoto demonstračního příkladu:
# Knihovny Numpy a matplotlib # # Jedenáctý demonstrační příklad: # - vykreslení průběhů několika funkcí # - do polárního grafu import numpy as np import matplotlib.pyplot as plt # úhel v polárním grafu theta = np.linspace(0.00, 4*np.pi, 150) # první funkce: vzdálenost od středu radius1 = theta # druhá funkce: vzdálenost od středu radius2 = 3*np.abs(theta-2*np.pi) ax=plt.subplot(111, projection="polar") # vykreslit průběh první funkce # v polárním grafu ax.plot(theta, radius2, "b", label="f1") # vykreslit průběh druhé funkce # v polárním grafu ax.fill(theta, radius1, "yellow", alpha=0.3, label="f1") # přidání legendy plt.legend(loc="lower left") # zobrazení grafu plt.show()
13. Předchozí části seriálu
- Vývojová prostředí ve Fedoře (1. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-1-dil/ - Vývojová prostředí ve Fedoře (2. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-2-dil/ - Vývojová prostředí ve Fedoře (3. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-3-dil/ - Vývojová prostředí ve Fedoře (4. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-4-dil/ - Integrovaná vývojová prostředí ve Fedoře: PyDev
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Integrovaná vývojová prostředí ve Fedoře: PyDev (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: IPython a IPython Notebook
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-ipython-a-ipython-notebook/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy-2-cast/
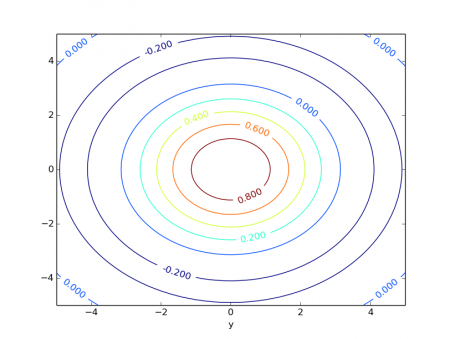
Obrázek 14: V navazujícím článku se seznámíme mj. i se způsobem vykreslování grafu s konturami, což je jedna z variant vizualizace funkcí se dvěma nezávislými proměnnými. Relativně snadno je však možné vytvářet i složitější 3D grafy, vyplněné kontury apod.
14. Odkazy na Internetu
- Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Systémy lineárních rovnic
http://www.matematika.cz/systemy-linearnich-rovnic - IPython homepage
http://ipython.org/ - Dokumentace k IPythonu
http://ipython.org/documentation.html# - IPython Tutorial
http://ipython.readthedocs.org/en/stable/interactive/tutorial.html - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb - 0MQ Home Page
http://zeromq.org/ - Is IPython Notebook ever used as an IDE, or merely for presentations?
https://www.reddit.com/r/IPython/comments/1uk7hp/is_ipython_notebook_ever_used_as_an_ide_or_merely/ - The IDE as a Bad Programming Language Enabler
https://dzone.com/articles/ide-bad-programming-language - Enhanced Interactive Python with IPython
http://www.onlamp.com/pub/a/python/2005/01/27/ipython.html - Direct mode
https://en.wikipedia.org/wiki/Direct_mode - Seznámení s Python IDE Spyder (článek vyšel zde na mojefedora.cz)
http://mojefedora.cz/seznameni-s-python-ide-spyder/ - Stránka s popisem různých IDE pro Python
http://quintagroup.com/cms/python/ide - Eclipse (stránka o frameworku na Fedoraproject.org)
https://fedoraproject.org/wiki/Eclipse - PyDev (hlavní stránka)
http://pydev.sourceforge.net/index.html - PyDev (download, v podstatě není zapotřebí)
http://pydev.sourceforge.net/download.html - PyDev (stránka s metainformacemi o PyDev pluginu, použita v Eclipse)
http://www.pydev.org/updates/ - PyDev (stránka s pluginem, použita v Eclipse)
https://dl.bintray.com/fabioz/pydev/4.5.4/ - Certifikát, který lze do Eclipse doinstalovat
http://www.pydev.org/pydev_certificate.cer - PyDev FAQ
http://pydev.sourceforge.net/faq.html - PyDev (Wikipedia)
https://en.wikipedia.org/wiki/PyDev - Python (oficiální stránky projektu)
https://www.python.org/ - Jython
http://www.jython.org/ - IronPython
http://ironpython.net/ - Python 3.5.1 documentation
https://docs.python.org/3/ - PyDev: Unittest integration
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Continuous unit testing with Pydev (Python and Eclipse)
http://stackoverflow.com/questions/1015581/continuous-unit-testing-with-pydev-python-and-eclipse - Test-driven development
https://en.wikipedia.org/wiki/Test-driven_development


