V poslední části článku o interaktivním i programovém použití knihoven Numpy a matplotlib si ukážeme způsob tvorby grafů s konturami („vrstevnicemi“), dále pak trojrozměrné grafy funkcí typu z=f(x,y) a na závěr si řekneme, jak se vytváří trojrozměrné grafy s funkcemi typu [x,y,z]=f(t).
Obsah
2. Použití funkce numpy.meshgrid()
3. Graf s konturami funkce z=f(x,y)
4. Přidání popisků k jednotlivým „vrstevnicím“
5. Další vylepšení grafu s konturami
6. Jednoduchý trojrozměrný graf funkce z=f(x,y) – drátový model
7. Od drátového modelu k vyplněné ploše
8. Zobrazení legendy – colorbaru
9. Promítnutí grafu na plochy kolmé na osy
10. Zobrazení 3D grafu funkce typu [x,y,z]=f(t)
12. Repositář s demonstračními příklady
1. Integrovaná vývojová prostředí ve Fedoře: vykreslování grafů s využitím knihoven Numpy a matplotlib (dokončení)
V závěrečné části článku o základních vlastnostech knihovny Matplotlib, zejména v kombinaci možností této knihovny s knihovnou Numpy, navážeme na část předchozí, protože si ukážeme tři možnosti tvorby grafů funkcí typu z=f(x,y), tj. funkcí se dvěma nezávislými proměnnými. Tyto funkce je možné zobrazit různým způsobem, například ve formě kontur („vrstevnic“), drátového modelu (wireframe) či dokonce vyplněné plochy (mapy výšek, heightfield). Na závěr si ukážeme způsob vykreslení funkcí typu [x,y,z]=f(t), což jsou funkce jediné nezávislé proměnné, ovšem graf této funkce je nutné zobrazit v trojrozměrném prostoru. Zajímavým příkladem podobné funkce (přesněji řečeno funkce, kde nové hodnoty [x,y,z] závisí na předchozích hodnotách) je takzvaný Lorenzův atraktor ukázaný v jedenácté kapitole.
Obrázek 1: Sloupcový graf s vyznačením odchylek či chyb, jehož tvorbu jsme si popsali v předchozím článku.
2. Použití funkce numpy.meshgrid()
Před popisem grafů zobrazujících drátové modely či kontury funkcí typu z=f(x,y) se musíme seznámit s užitečnou funkcí nazvanou numpy.meshgrid(). Tato funkce má sice poměrně univerzální možnosti použití, my se však v dnešním článku spokojíme s tím, že pokud se funkci numpy.meshgrid() předá dvojice jednorozměrných polí (vektorů) představujících hodnoty nezávislých x-ových a y-ových souřadnic, vytvoří se jako výsledek dvě dvourozměrné matice, které dohromady tvoří mřížku souřadnic [xi, yi]. Počet řádků těchto 2D matic odpovídá délce druhého pole, počet sloupců pak délce pole prvního. Podívejme se na jednoduchý příklad:
# vytvoření vektoru [1..10]
x=np.arange(1, 11, 1)
# vytvoření vektoru [101..105]
y=np.arange(101, 106, 1)
# zobrazení prvního vektoru
x
array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# zobrazení druhého vektoru
y
array([101, 102, 103, 104, 105])
# zavolání funkce numpy.meshgrid
np.meshgrid(x,y)
[array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]),
array([[101, 101, 101, 101, 101, 101, 101, 101, 101, 101],
[102, 102, 102, 102, 102, 102, 102, 102, 102, 102],
[103, 103, 103, 103, 103, 103, 103, 103, 103, 103],
[104, 104, 104, 104, 104, 104, 104, 104, 104, 104],
[105, 105, 105, 105, 105, 105, 105, 105, 105, 105]])]
Většinou se první i druhá matice uloží do samostatné proměnné, a to následovně (povšimněte si, že výsledné matice jsou uloženy do proměnných označených verzálkami):
# uložení první matice do proměnné X
# uložení druhé matice do proměnné Y
X,Y=np.meshgrid(x,y)
# zobrazení první matice
X
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
# zobrazení druhé matice
Y
array([[101, 101, 101, 101, 101, 101, 101, 101, 101, 101],
[102, 102, 102, 102, 102, 102, 102, 102, 102, 102],
[103, 103, 103, 103, 103, 103, 103, 103, 103, 103],
[104, 104, 104, 104, 104, 104, 104, 104, 104, 104],
[105, 105, 105, 105, 105, 105, 105, 105, 105, 105]])
Z předchozích částí tohoto seriálu již víme, že s maticemi je možné mj. provádět i základní operace typu součet matic, rozdíl matic, maticový součin atd. Taktéž je možné na prvky matice aplikovat logaritmické či goniometrické funkce, takže například následující zápis je zcela korektní:
# součet matic a následně aplikace goniometrické funkce sin
# na každý prvek výsledné matice
Z=np.sin(X+Y)
# podívejme se na výslednou matici
Z
array([[ 0.99482679, 0.62298863, -0.3216224 , -0.97053528, -0.7271425 ,
0.18478174, 0.92681851, 0.81674261, -0.04424268, -0.86455145],
[ 0.62298863, -0.3216224 , -0.97053528, -0.7271425 , 0.18478174,
0.92681851, 0.81674261, -0.04424268, -0.86455145, -0.8899956 ],
[-0.3216224 , -0.97053528, -0.7271425 , 0.18478174, 0.92681851,
0.81674261, -0.04424268, -0.86455145, -0.8899956 , -0.09718191],
[-0.97053528, -0.7271425 , 0.18478174, 0.92681851, 0.81674261,
-0.04424268, -0.86455145, -0.8899956 , -0.09718191, 0.78498039],
[-0.7271425 , 0.18478174, 0.92681851, 0.81674261, -0.04424268,
-0.86455145, -0.8899956 , -0.09718191, 0.78498039, 0.94543533]])
Obrázek 2: Koláčový graf, jehož tvorbu jsme si popsali v předchozím článku.
3. Graf s konturami funkce z=f(x,y)
První způsob zobrazení funkce typu z=f(x,y) spočívá ve vykreslení takzvaných kontur, které si pro zjednodušení můžeme představit jako vrstevnice na mapě – body spojené konturou/vrstevnicí mají stejnou hodnotu funkce (tj. stejnou hodnotu z-ové souřadnice). Při vyhodnocování a následném vykreslení funkce budeme postupovat následovně:
- Vytvoříme vektor s hodnotami nezávislé proměnné x.
- Vytvoříme vektor s hodnotami nezávislé proměnné y.
- S využitím numpy.meshgrid necháme vygenerovat dvojici matic souřadnic.
- Necháme vypočítat body ležící na ploše funkce (z-ové souřadnice se uloží do matice Z).
- Vlastní vykreslení kontur zajistí funkce matplotlib.pyplot.contour(X, Y, Z).
Podívejme se na úplný příklad:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # Dvacátý první demonstrační příklad: # - zobrazení kontur funkce typu z=f(x,y) import matplotlib import numpy as np import matplotlib.cm as cm # není nutné, použijeme v dalším příkladu import matplotlib.mlab as mlab # není nutné, použijeme v dalším příkladu import matplotlib.pyplot as plt delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R1 = np.sqrt(X*X+Y*Y) # vzdálenost od bodu [3,3] R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3)) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R1)-np.cos(R2) # povolení zobrazení mřížky plt.grid(True) # vytvoření grafu s konturami funkce z=f(x,y) plt.contour(X, Y, Z) # zobrazení grafu plt.show()
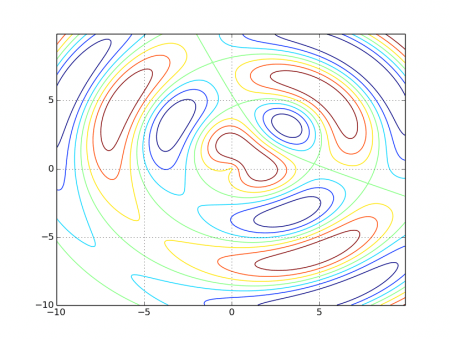
Obrázek 3: Zobrazení kontur funkce typu z=f(x,y).
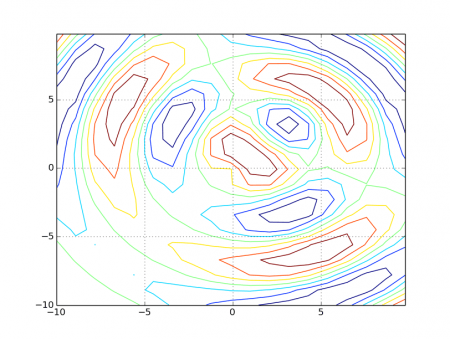
Obrázek 4: Pokud je hodnota „delta“ příliš vysoká, vypočte se menší počet bodů tvořících plochu funkce, takže i kontury budou vykresleny velmi nepřesně (knihovna bude mít k dispozici jen málo bodů, které bude moci spojit).
4. Přidání popisků k jednotlivým „vrstevnicím“
Další vylepšení spočívá v přidání popisků (výšek) jednotlivých kontur/vrstevnic, což je opět způsob, který čtenáři pravděpodobně znají z běžných map. Jakmile je graf funkce vykreslen, postačuje zavolat funkci nazvanou plt.clabel(), které se předá proměnná obsahující všechny informace o právě vytvořeném grafu. Tato funkce taktéž akceptuje množství parametrů popsaných na stránce http://matplotlib.org/api/pyplot_api.html?highlight=contour#matplotlib.pyplot.contour. My nastavíme parametr inline na hodnotu True (pod textem se nezobrazí kontura, to by bylo poměrně nečitelné) a parametr fontsize na požadovanou relativní velikost písma s popisky:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # Dvacátý druhý demonstrační příklad: # - zobrazení kontur funkce typu z=f(x,y) # - zobrazení hodnot u jednotlivých "vrstevnic" import matplotlib import numpy as np import matplotlib.cm as cm # není nutné, použijeme v dalším příkladu import matplotlib.mlab as mlab # není nutné, použijeme v dalším příkladu import matplotlib.pyplot as plt delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R1 = np.sqrt(X*X+Y*Y) # vzdálenost od bodu [3,3] R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3)) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R1)-np.cos(R2) # povolení zobrazení mřížky plt.grid(True) # vytvoření grafu s konturami funkce z=f(x,y) CS = plt.contour(X, Y, Z) # popisky "vrstevnic" plt.clabel(CS, inline=1, fontsize=10) # zobrazení grafu plt.show()
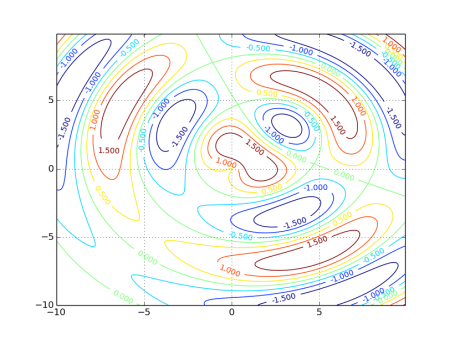
Obrázek 5: U jednotlivých „vrstevnic“ je uvedena i jejich hodnota odpovídající hodnotě funkce v daném bodě.
5. Další vylepšení grafu s konturami
Další vylepšení, které může být výhodné zejména ve chvíli, kdy jsou plochy s konturami vybarveny (pro vybarvení použijte funkci matplotlib.pyplot.contourf namísto pouhého matplotlib.pyplot.countour) spočívá v přidání legendy, na níž se zobrazují výšky jednotlivých kontur/vrstevnic. Přidání je jednoduché, stačí pouze použít funkci nazvanou matplotlib.pyplot.colorbar(), které se opět předá datová struktura reprezentující graf funkce a několik nepovinných pojmenovaných parametrů. Z těchto parametrů dnes použijeme pouze parametr nazvaný shrink (relativní velikost popisku) a extend (způsob vykreslení popisků vedle grafu). Podívejme se na úplný zdrojový kód příkladu:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # Dvacátý třetí demonstrační příklad: # - zobrazení kontur funkce typu z=f(x,y) # - zobrazení hodnot u jednotlivých "vrstevnic" # - přidání legendy import matplotlib import numpy as np import matplotlib.cm as cm # není nutné, použijeme v dalším příkladu import matplotlib.mlab as mlab import matplotlib.pyplot as plt delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R1 = np.sqrt(X*X+Y*Y) # vzdálenost od bodu [3,3] R2 = np.sqrt((X-3)*(X-3)+(Y-3)*(Y-3)) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R1)-np.cos(R2) # povolení zobrazení mřížky plt.grid(True) # vytvoření grafu s konturami funkce z=f(x,y) CS = plt.contour(X, Y, Z) # přidání legendy (colorbar) CB = plt.colorbar(CS, shrink=0.7, extend='both') # popisky "vrstevnic" plt.clabel(CS, inline=1, fontsize=10) # zobrazení grafu plt.show()
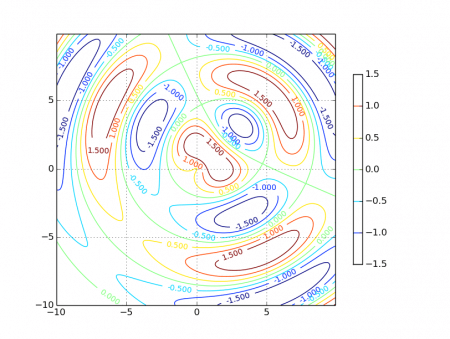
Obrázek 6: Kromě vrstevnic a jejich hodnot se napravo od grafu zobrazila i „mapa výšek“. Relativní velikost mapy vůči celému grafu se řídí hodnotou shrink. Zde konkrétně má celá legenda výšku jen 70% výšky celého grafu.
6. Jednoduchý trojrozměrný graf funkce z=f(x,y) – drátový model
Použití grafu s konturami sice může být v mnoha ohledech velmi užitečné (například při zjišťování lokálních minim a maxim), v praxi se však spíše setkáme s odlišným typem grafů zobrazujících funkce typu z=f(x,y). Jedná se o trojrozměrné grafy, v nichž se zobrazuje plocha funkce. Nejjednodušším typem tohoto grafu je takzvaný drátový model, který je spíše známý pod svým anglickým názvem wireframe. V tomto typu grafu je zobrazena série křivek či spíše lomených čar. Jedna série je vypočtena takovým způsobem, že x-ová souřadnice se postupně mění v nastaveném intervalu zatímco y-ová souřadnice je konstantní. Druhá série lomených čar se vykresluje kolmo na sérii první, tj. x-ová souřadnice je konstantní a postupně se mění hodnota y-ových souřadnic. Výsledkem je tedy plocha, která má při pohledu z osy z tvar pravidelné mřížky. Pro vykreslení tohoto typu grafu se používá funkce plot_wireframe(), které se předá trojice polí odpovídajících x-ovým, y-ovým a z-ovým souřadnicím bodů ležících na ploše představujících obraz funkce:
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # Dvacátý čtvrtý demonstrační příklad: # - zobrazení 3D grafu funkce typu z=f(x,y) from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt import numpy as np fig = plt.figure() ax = fig.add_subplot(111, projection='3d') delta = 0.1 # průběh nezávislé proměnné x x = np.arange(-10.0, 10.0, delta) # průběh nezávislé proměnné y y = np.arange(-10.0, 10.0, delta) # vytvoření dvou polí se souřadnicemi [x,y] X, Y = np.meshgrid(x, y) # vzdálenost od bodu [0,0] R = np.sqrt(X*X+Y*Y) # výpočet funkce, kterou použijeme při vykreslování grafu Z = np.sin(R)/R # zobrazení 3D grafu ax.plot_wireframe(X, Y, Z, rstride=7, cstride=7) # zobrazení grafu plt.show()
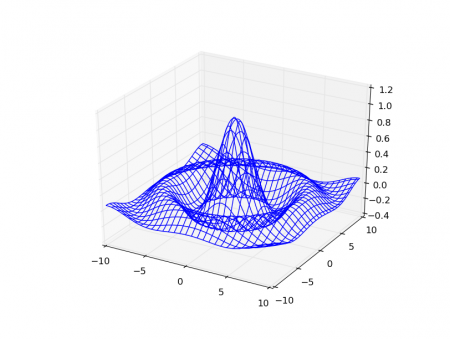
Obrázek 7: Drátový model vykreslený s využitím funkce plot_wireframe(X, Y, Z, rstride=7, cstride=7).
Pojmenované parametry rstride a cstride lze použít pro řízení hustoty vykreslované mřížky. Tyto parametry představují krok použitý při změně x-ových a y-ových souřadnic, což znamená, že čím menší hodnota se požije, tím bode vykreslená mřížka jemnější:
ax.plot_wireframe(X, Y, Z, rstride=3, cstride=3)
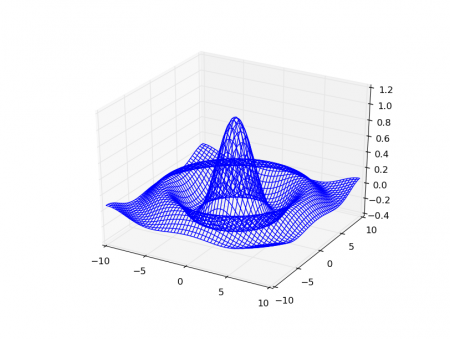
Obrázek 8: Drátový model vykreslený s využitím funkce plot_wireframe(X, Y, Z, rstride=3, cstride=3).
7. Od drátového modelu k vyplněné ploše
Drátový model je možné v případě potřeby nahradit vykreslením vyplněné plochy namísto pouhé mřížky. V tomto případě je nutné namísto funkce plot_wireframe() použít funkci pojmenovanou plot_surface(). První tři povinné parametry obou zmíněných funkcí jsou shodné, dokonce lze použít i stejně pojmenované parametry cstride a rstride, o jejichž významu jsme se taktéž zmiňovali. Kromě toho se však navíc většinou používá i další pojmenovaný parametr cmap, kterému se předá barvová paleta (či barvová mapa), která typicky definuje jeden gradientní přechod i větší množství gradientních přechodů mezi různými odstíny. Pro účely vytváření gradientních přechodů či pro použití již předem připravených barvových map se používá modul matplotlib.cm. Seznam všech předdefinovaných barvových map naleznete na adrese https://gist.github.com/endolith/2719900#id7, ukázky (palety) pak na adrese http://matplotlib.org/examples/color/colormaps_reference.html. My využijeme barvovou mapu pojmenovanou „coolwarm“:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# Dvacátý pátý demonstrační příklad:
# - zobrazení 3D grafu funkce typu z=f(x,y)
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y)
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
# zobrazení 3D grafu formou plochy
ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# zobrazení grafu
plt.show()
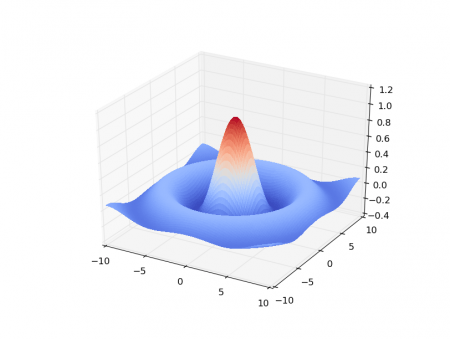
Obrázek 9: Plocha funkce z=f(x,y) používající barvovou mapu pojmenovanou „coolwarm“.
8. Zobrazení legendy – colorbaru
O způsobu zobrazení takzvaného colorbaru jsme se již zmínili v páté kapitole v souvislosti s grafem zobrazujícím kontury. Ovšem colorbar má svůj význam i v případě 3D grafů, což ostatně uvidíme po spuštění následujícího demonstračního příkladu, v němž se napravo od grafu s plochou funkce z=f(x,y) zobrazí i „mapa výšek“. Povšimněte si způsobu nastavení měřítka z-ové osy funkcí set_zlim() a taktéž změny způsobu formátování výšek, tj. popisu z-ové osy (set_major_locator() a set_major_formatter()):
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# Dvacátý šestý demonstrační příklad:
# - zobrazení 3D grafu funkce typu z=f(x,y)
# - pomocná legenda - colorbar
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.pyplot as plt
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y)
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
# zobrazení 3D grafu formou plochy
surface = ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_zlim(-1.01, 1.01)
# styl formátování popisků
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
# přidání pomocné legendy
fig.colorbar(surface, shrink=0.7, aspect=5)
# zobrazení grafu
plt.show()
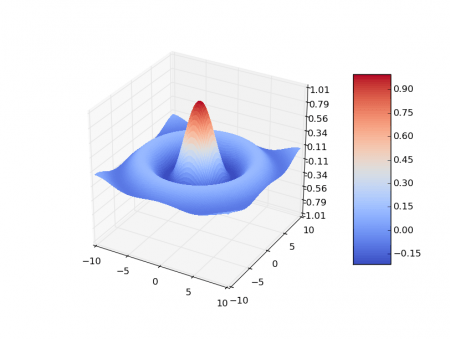
Obrázek 10: Plocha funkce z=f(x,y) používající barvovou mapu pojmenovanou „coolwarm“. Vedle grafu je zobrazena i legenda
9. Promítnutí grafu na plochy kolmé na osy
Vzhledem k tomu, že se pro zobrazení trojrozměrného grafu na 2D obrazovce musí používat axonometrické promítání popř. promítání s perspektivou, nemusí být z obrázku na první pohled zřejmé, jak přesně vlastně průběh funkce vypadá. Knihovna Matplotlib nám však nabízí řešení – na plochy (které jsou kolmé na osy souřadného systému) se promítnou kontury průběhu funkce. Podívejme se, jak vypadá výsledek:
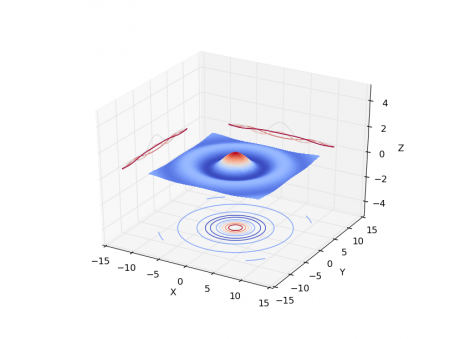
Obrázek 11: Promítnutí kontur průběhu funkce na plochy..
Samotná plocha představující funkci se vykreslí příkazem matplotlib.pyplot.plot_surface(), podobně jako v předchozím příkladu. Dále se metodou ax.contour() mohou vykreslit kontury grafu na jednotlivé plochy, ve skutečnosti je však ještě nutné korektně nastavit přesné umístění těchto kontur do grafu. K tomu slouží explicitní nastavení rozsahů na jednotlivých osách (set_xlim(), set_ylim(), set_zlim()) a vlastní posun reprezentovaný pojmenovaným parametrem offset předaným do metody ax.contour(). Podívejme se na odladěný příklad:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# Dvacátý sedmý demonstrační příklad:
# - zobrazení 3D grafu funkce typu z=f(x,y)
# - pomocná legenda - colorbar
# - promítnutí grafu na ploch kolmých na osy
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
delta = 0.1
# průběh nezávislé proměnné x
x = np.arange(-10.0, 10.0, delta)
# průběh nezávislé proměnné y
y = np.arange(-10.0, 10.0, delta)
# vytvoření dvou polí se souřadnicemi [x,y]
X, Y = np.meshgrid(x, y)
# vzdálenost od bodu [0,0]
R = np.sqrt(X*X+Y*Y)
# výpočet funkce, kterou použijeme při vykreslování grafu
Z = np.sin(R)/R
# zobrazení 3D grafu formou plochy
surface = ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# kontutra: průmět na rovinu x-y
cset = ax.contour(X, Y, Z, zdir='z', offset=-5, cmap=cm.coolwarm)
# kontutra: průmět na rovinu y-z
cset = ax.contour(X, Y, Z, zdir='x', offset=-15, cmap=cm.coolwarm)
# kontutra: průmět na rovinu x-z
cset = ax.contour(X, Y, Z, zdir='y', offset= 15, cmap=cm.coolwarm)
# rozměry grafu ve směru osy x
ax.set_xlabel('X')
ax.set_xlim(-15, 15)
# rozměry grafu ve směru osy y
ax.set_ylabel('Y')
ax.set_ylim(-15, 15)
# rozměry grafu ve směru osy z
ax.set_zlabel('Z')
ax.set_zlim(-5, 5)
# zobrazení grafu
plt.show()
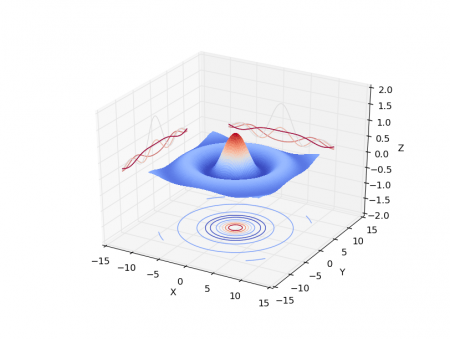
Obrázek 12: Změna měřítka ve směru osy z. Při změně měřítka je současně nutné posunout konturu pojmenovaným parametrem offset.
10. Zobrazení 3D grafu funkce typu [x,y,z]=f(t)
Další typ grafu, s nímž se dnes seznámíme, je trojrozměrný graf, v němž se zobrazuje funkce typu [x,y,z]=f(t) popř. složitější funkce [xn, yn, zn]=f(xn-1, yn-1, zn-1). O zobrazení průběhů těchto funkcí se stará matplotlib.pyplot.plot(), s níž jsme se již seznámili v předchozích částech tohoto seriálu. Tento příkaz automaticky zjistí potřebné rozsahy na všech třech osách, což je dobře patrné ze screenshotu číslo 13. Podívejme se tedy, jakým způsobem je možné zobrazit trojrozměrnou spirálu (pokud budete potřebovat, aby se spirála nezužovala, postačuje proměnnou r nastavit na konstantní hodnotu):
#!/usr/bin/env python # Knihovny Numpy a matplotlib # # Dvacátý osmý demonstrační příklad: # - zobrazení 3D grafu funkce typu [x,y,z]=f(t) from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt import numpy as np # nezávislá proměnná t = np.arange(0, 8*np.pi, 0.1) # vzdálenost od osy spirály r = 10.0/(t+4) # výpočet souřadnic [x,y,z]) pro každé t x = r*np.cos(t) y = r*np.sin(t) z = t fig = plt.figure() ax = fig.gca(projection='3d') # vykreslení grafu ax.plot(x, y, z) # zobrazení grafu plt.show()
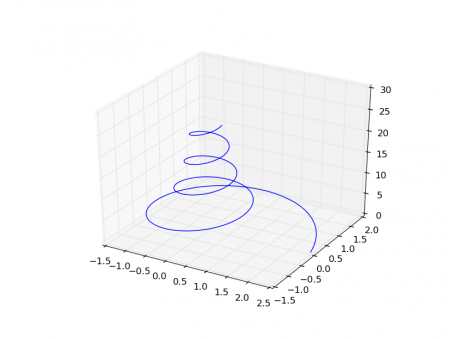
Obrázek 13: Spirála vykreslená předchozím demonstračním příkladem.
11. Lorenzův atraktor
Poměrně vděčným příkladem funkce zobrazené v 3D prostoru je dynamický systém s takzvaným podivným atraktorem, který je nazvaný Lorenzův atraktor podle svého objevitele. Tento systém sestávající ze tří dynamických rovnic použil Edward Lorenz v roce 1963 při simulaci vývoje počasí (resp. ve velmi zjednodušeném modelu počasí). Na tomto systému byla také numericky a analyticky ověřena velká citlivost na počáteční podmínky (někdy také nazývaná „motýlí efekt“). Pro upřesnění je však nutné říci, že při simulaci na počítači vlastně získáme atraktor, jenž je periodický. Je to z toho důvodu, že pro zobrazení číselných hodnot je použito konečného počtu bitů, z toho nutně vyplývá, že se po určitém počtu kroků (který je však obrovský, takže tento jev mnohdy nezaregistrujeme) začne dráha Lorenzova atraktoru překrývat. V matematicky přesném modelu však tato situace nenastane, každá smyčka funkce bude mít unikátní tvar a dráhy se nebudou překrývat, pouze protínat. Diferenciální rovnice Lorenzova atraktoru mají po převodu na diferenční tvar následující formát:
dx/dt = σ (y-x) dy/dt = x(ρ - z) - y dz/dt = xy - Βz
Takže pro iterativní (samozřejmě že nepřesný) výpočet můžeme pracovat s následujícími vztahy, které pro dostatečně malé dt vedou k výpočtu bodů ležících na Lorenzově atraktoru:
xn+1=xn+(σ (y-x)) dt yn+1=yn+(x(ρ - z) - y) dt zn+1=zn+(xy - Βz) dt
Podívejme se nyní na způsob implementace této funkce:
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
A výpočtu sekvence bodů ležících na atraktoru:
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru (resp. bodů na něm ležících)
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
Vlastní zobrazení pak probíhá naprosto stejným způsobem, jako tomu bylo v předchozím demonstračním příkladu:
#!/usr/bin/env python
# Knihovny Numpy a matplotlib
#
# Dvacátý devátý demonstrační příklad:
# - Lorenzův atraktor
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
# funkce pro výpočet dalšího bodu Lorenzova atraktoru
def lorenz(x, y, z, s=10, r=28, b=2.667):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# krok (změna času)
dt = 0.01
# celkový počet vypočtených bodů na Lorenzově atraktoru
n = 10000
# prozatím prázdné pole připravené pro výpočet
x = np.zeros((n,))
y = np.zeros((n,))
z = np.zeros((n,))
# počáteční hodnoty
x[0], y[0], z[0] = (0., 1., 1.05)
# vlastní výpočet atraktoru
for i in range(n-1):
x_dot, y_dot, z_dot = lorenz(x[i], y[i], z[i])
x[i+1] = x[i] + x_dot * dt
y[i+1] = y[i] + y_dot * dt
z[i+1] = z[i] + z_dot * dt
fig = plt.figure()
ax = fig.gca(projection='3d')
# vykreslení grafu
ax.plot(x, y, z)
# zobrazení grafu
plt.show()
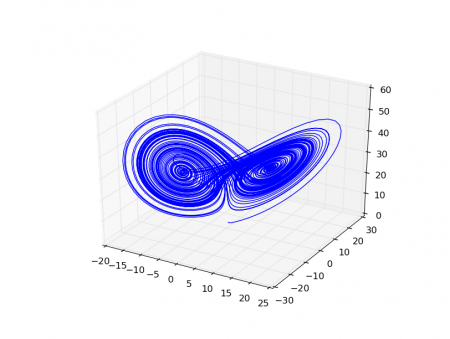
Obrázek 14: Lorenzův atraktor vykreslený předchozím demonstračním příkladem.
12. Repositář s demonstračními příklady
Všechny demonstrační příklady, s nimiž jsme se dnes seznámili, byly uloženy do Git repositáře umístěného na GitHubu (https://github.com/tisnik/presentations). Poslední verze zdrojových kódů naleznete pod odkazy uvedenými v tabulce pod tímto odstavcem:
Obrázek 15: Vykreslení průběhu tří funkcí. Ve skutečnosti se však pro každou funkci vypočte pouze sto bodů, které jsou propojeny úsečkami. Díky velké hustotě bodů není (alespoň na těchto funkcích) náhrada hladkých křivek za lomenou čáru viditelné (viz též předchozí část tohoto seriálu)j.
13. Předchozí části seriálu
- Vývojová prostředí ve Fedoře (1. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-1-dil/ - Vývojová prostředí ve Fedoře (2. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-2-dil/ - Vývojová prostředí ve Fedoře (3. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-3-dil/ - Vývojová prostředí ve Fedoře (4. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-4-dil/ - Integrovaná vývojová prostředí ve Fedoře: PyDev
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Integrovaná vývojová prostředí ve Fedoře: PyDev (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: IPython a IPython Notebook
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-ipython-a-ipython-notebook/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: vykreslování grafů s využitím knihoven Numpy a matplotlib
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-vykreslovani-grafu-s-vyuzitim-knihoven-numpy-a-matplotlib/ - Integrovaná vývojová prostředí ve Fedoře: vykreslování grafů s využitím knihoven Numpy a matplotlib (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-vykreslovani-grafu-s-vyuzitim-knihoven-numpy-a-matplotlib-2-cast/
14. Odkazy na Internetu
- Lorenzův atraktor
http://www.root.cz/clanky/fraktaly-v-pocitacove-grafice-iii/#k03 - Popis barvových map modulu matplotlib.cm
https://gist.github.com/endolith/2719900#id7 - Ukázky (palety) barvových map modulu matplotlib.cm
http://matplotlib.org/examples/color/colormaps_reference.html - Lorenz system
https://en.wikipedia.org/wiki/Lorenz_system - Customising contour plots in matplotlib
https://philbull.wordpress.com/2012/12/27/customising-contour-plots-in-matplotlib/ - Graphics with Matplotlib
http://kestrel.nmt.edu/~raymond/software/python_notes/paper004.html - Systémy lineárních rovnic
http://www.matematika.cz/systemy-linearnich-rovnic - IPython homepage
http://ipython.org/ - Dokumentace k IPythonu
http://ipython.org/documentation.html# - IPython Tutorial
http://ipython.readthedocs.org/en/stable/interactive/tutorial.html - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb - 0MQ Home Page
http://zeromq.org/ - Is IPython Notebook ever used as an IDE, or merely for presentations?
https://www.reddit.com/r/IPython/comments/1uk7hp/is_ipython_notebook_ever_used_as_an_ide_or_merely/ - The IDE as a Bad Programming Language Enabler
https://dzone.com/articles/ide-bad-programming-language - Enhanced Interactive Python with IPython
http://www.onlamp.com/pub/a/python/2005/01/27/ipython.html - Direct mode
https://en.wikipedia.org/wiki/Direct_mode - Seznámení s Python IDE Spyder (článek vyšel zde na mojefedora.cz)
http://mojefedora.cz/seznameni-s-python-ide-spyder/ - Stránka s popisem různých IDE pro Python
http://quintagroup.com/cms/python/ide - Eclipse (stránka o frameworku na Fedoraproject.org)
https://fedoraproject.org/wiki/Eclipse - PyDev (hlavní stránka)
http://pydev.sourceforge.net/index.html - PyDev (download, v podstatě není zapotřebí)
http://pydev.sourceforge.net/download.html - PyDev (stránka s metainformacemi o PyDev pluginu, použita v Eclipse)
http://www.pydev.org/updates/ - PyDev (stránka s pluginem, použita v Eclipse)
https://dl.bintray.com/fabioz/pydev/4.5.4/ - Certifikát, který lze do Eclipse doinstalovat
http://www.pydev.org/pydev_certificate.cer - PyDev FAQ
http://pydev.sourceforge.net/faq.html - PyDev (Wikipedia)
https://en.wikipedia.org/wiki/PyDev - Python (oficiální stránky projektu)
https://www.python.org/ - Jython
http://www.jython.org/ - IronPython
http://ironpython.net/ - Python 3.5.1 documentation
https://docs.python.org/3/ - PyDev: Unittest integration
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Continuous unit testing with Pydev (Python and Eclipse)
http://stackoverflow.com/questions/1015581/continuous-unit-testing-with-pydev-python-and-eclipse - Test-driven development
https://en.wikipedia.org/wiki/Test-driven_development


