Ve druhém článku o fyzikálním enginu, který je součástí knihovny LÖVE, si na čtveřici demonstračních příkladů ukážeme použití jiných tvarů těles v simulovaném světě, seznámíme se s konceptem takzvaných obalových těles používaných při detekci kolizí a taktéž se způsobem řešení některých problémů plynoucích z nepřesných výpočtů těchto kolizí.
Obsah
1. Fyzikální engine implementovaný v knihovně LÖVE (2.část)
2. Použití dalších tvarů těles v simulovaném světě
3. Zdrojový kód prvního demonstračního příkladu
4. Detekce kolizí a obalová tělesa používaná v knihovně LÖVE
5. Zdrojový kód druhého demonstračního příkladu
6. Problematika „průstřelu“ tenkých stěn a způsob jejího řešení
7. Zdrojový kód třetího demonstračního příkladu
8. Použití přesnějšího výpočtu kolizí
9. Zdrojový kód čtvrtého demonstračního příkladu
10. Repositář se zdrojovými kódy všech čtyř dnešních demonstračních příkladů
1. Fyzikální engine implementovaný v knihovně LÖVE (2.část)
V prvním článku o fyzikálním enginu implementovaném v knihovně LÖVE jsme si řekli základní informace o tom, k čemu se vlastně tento engine využívá a jakým způsobem je ho možné zařadit do vyvíjených aplikací napsaných v programovacím jazyku Lua. Taktéž jsme se seznámili se základními typy objektů, s nimiž tento engine pracuje a z nichž se vytváří simulovaný (například herní) svět. Připomeňme si tedy jen ve stručnosti, že fyzikální engine je v knihovně LÖVE dostupný přes modul pojmenovaný love.physics a – podobně jako celá knihovna LÖVE – je orientován téměř výhradně na dvoudimenzionální (2D) grafiku. Díky omezení počtu rozměrů bylo možné všechny výpočty dynamiky těles urychlit a navíc je celé programové rozhraní modulu love.physics poměrně snadno pochopitelné, a to i pro začátečníky (na tomto místě je vhodné si uvědomit, že samotný engine je interně dosti složitý, ovšem úlohou správně navrženého API je tuto složitost od uživatelů odstínit, což se v tomto případě podařilo, i tak je však love.physics nejrozsáhlejším modulem v celé knihovně LÖVE).
Obrázek 1: Jednoduchá simulace vytvořená s využitím modulu love.physics.
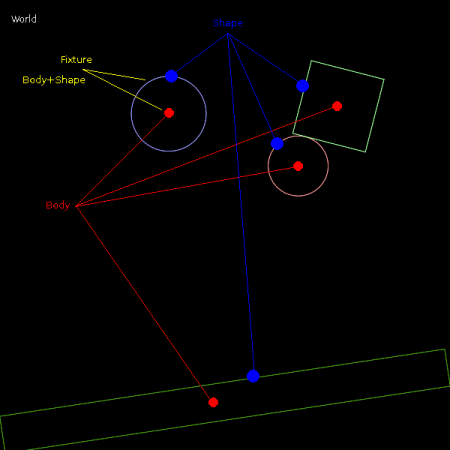
V předchozím článku jsme se taktéž dozvěděli, že celý simulovaný svět i všechna tělesa, která se v tomto světě pohybují, se popisuje pomocí následujících pěti typů objektů:
| # | Typ | Význam |
|---|---|---|
| 1 | World | objekt představující celý simulovaný dvourozměrný svět |
| 2 | Body | objekt představující nestlačitelnou hmotu v simulovaném světě |
| 3 | Shape | geometrický tvar přiřazený k tělesu |
| 4 | Fixture | vazba mezi již vytvořeným tvarem (shape) a tělesem (body) |
| 5 | Joint | vazba mezi tělesy, které se nachází v simulovaném světě |
Obrázek 2: Vztah mezi čtyřmi základními typy objektů: World, Body(ies), Shape(s) a Fixture(s), bližší informace viz první článek na toto téma.
2. Použití dalších tvarů těles v simulovaném světě
V předchozích dvou demonstračních příkladech byly použity statické i pohybující se objekty, jejichž tvar (shape) odpovídal obdélníkům. Jedná se o jeden z nejjednodušších tvarů, s nímž může engine love.physics pracovat, pro většinu aplikací by to ale bylo zcela nedostatečné. Proto jsou k dispozici i další tvary. Všechny dostupné tvary i jejich konstruktory (tj. funkce volané pro jejich vytvoření) jsou pro přehlednost vypsány v následující tabulce:
| # | Tvar | Konstruktor | Popis |
|---|---|---|---|
| 1 | rectangle | love.physics.newRectangleShape() | obdélník či čtverec (libovolně natočený) |
| 2 | polygon | love.physics.newPolygonShape() | konvexní polygon s maximálně osmi vrcholy |
| 3 | circle | love.physics.newCircleShape() | kruh/kružnice |
| 4 | edge | love.physics.newEdgeShape() | jen úsečka, tento tvar nemá vnitřek, omezené použití |
| 5 | chain | love.physics.newChainShape() | polyčára, tento tvar nemá vnitřek, omezené použití |
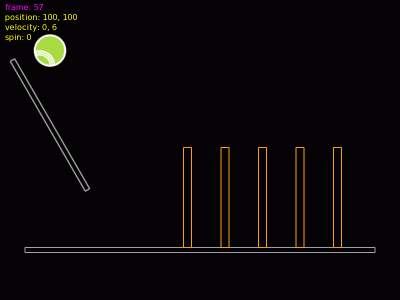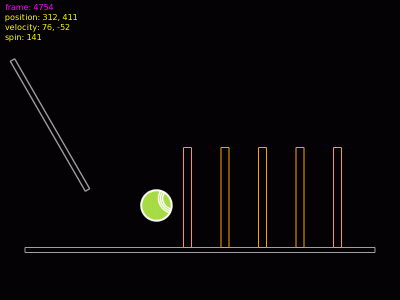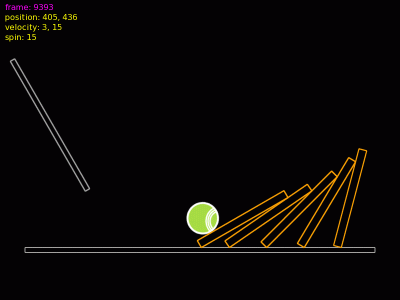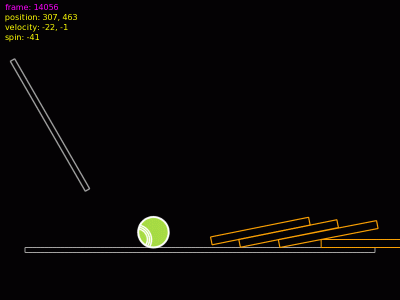
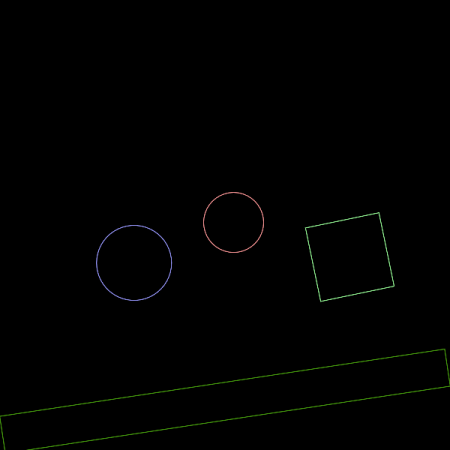
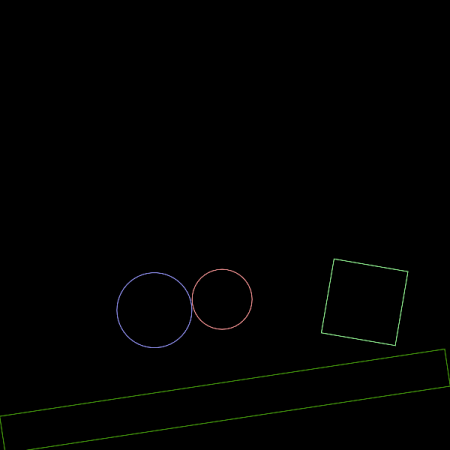
Obrázek 3: V tomto simulovaném světě se používají pouze tělesa s tvarem obdélníku.
Poznámka 1: pro pohybující se objekty je možné reálně využít jen první tři tvary: rectangle (speciální typ polygonu), konvexní polygon a circle. Další dva tvary jsou určeny pro nehybná tělesa, takže je možné je použít například pro vymodelování terénu. Zajímavý a potenciálně užitečný je v tomto ohledu tvar edge shape, který nemusí být konvexní, na rozdíl od tvaru polygon (a samozřejmě automaticky též rectangle).
Poznámka 2: v modulu love.physics se žádným způsobem neřeší způsob vykreslení tvarů na obrazovku. Tuto činnost musí explicitně zajistit programátor a to typicky takovým způsobem, že s využitím metod objekt.shape:getPoints(), objekt.body:getX(), objekt.body:getY() a objekt.body:getRadius() přečte aktuální pozici a rozměry tvaru, které následně předá do kreslicích funkcí modulu love.graphics. Alternativně je samozřejmě možné pouze získat pozici tvaru a vykreslit zcela odlišný objekt, například sprite. Volání zmíněných funkcí se většinou provádí v callback funkci love.draw, což použijeme i v demonstračních příkladech.
Obrázek 4: V další simulaci se již používají i kulatá tělesa.
3. Zdrojový kód prvního demonstračního příkladu
Použití dalších tvarů těles, zde konkrétně tvaru kruhu/kružnice, je ukázáno v dnešním prvním demonstračním příkladu. Ten je založen na obou příkladech, s nimiž jsme se seznámili minule, ovšem do simulovaného světa byly přidány dva míčky:
--
-- Funkce volaná při inicializaci aplikace.
--
function love.load()
...
...
...
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 400, 100, "dynamic")
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(40)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.9)
-- těleso představující druhý míček
objects.ball2 = {}
-- počáteční umístění tělesa
objects.ball2.body = love.physics.newBody(world, 225, 50, "dynamic")
-- tvar a rozměry
objects.ball2.shape = love.physics.newCircleShape(50)
-- propojení tvaru s tělesem
objects.ball2.fixture = love.physics.newFixture(objects.ball2.body, objects.ball2.shape, 5000)
objects.ball2.fixture:setRestitution(0.1)
...
...
...
end
Tyto míčky se v callback funkci love.draw() vykreslí velmi snadno s využitím metod pro přečtení aktuální souřadnice středu a poloměru zmíněných v předchozí kapitole:
--
-- Tato funkce je volána automaticky při překreslení obsahu
-- okna či obrazovky.
--
function love.draw()
...
...
...
-- vykreslení prvního tělesa (míčku)
love.graphics.setColor(250, 150, 150)
love.graphics.circle("line", objects.ball1.body:getX(), objects.ball1.body:getY(),
objects.ball1.shape:getRadius())
-- vykreslení druhého tělesa (míčku)
love.graphics.setColor(150, 150, 250)
love.graphics.circle("line", objects.ball2.body:getX(), objects.ball2.body:getY(),
objects.ball2.shape:getRadius())
...
...
...
end
Obrázek 5: Svět simulovaný v dnešním prvním demonstračním příkladu.
Úplný zdrojový kód demonstračního příkladu:
--
-- Knihovna LÖVE
--
-- Dvacátý demonstrační příklad
--
-- Jednoduchý "svět", v němž se nachází dva míčky a jeden kvádr.
--
-- rozměry okna, do něhož se bude provádět vykreslování
width = 600
height = 600
ground_height = 50
-- tíhové zrychlení
G = 9.81
-- počet pixelů odpovídající jednomu metru v simulovaném světě
pixels_per_meter = 64
--
-- Funkce volaná při inicializaci aplikace.
--
function love.load()
-- načtení standardního fontu a nastavení grafického režimu
local font = love.graphics.newFont(love.default_font, 40)
-- inicializace grafického režimu
love.graphics.setMode(width, height, false, false, 0)
-- nastavení rozměrů simulovaného světa
-- (mapování fyzikálních jednotek na pixely)
love.physics.setMeter(pixels_per_meter)
-- vytvoření simulovaného světa
world = love.physics.newWorld(0, G * pixels_per_meter, true)
-- tabulka s tělesy
objects = {}
-- těleso představující zemi
objects.ground = {}
-- počáteční umístění tělesa
objects.ground.body = love.physics.newBody(world, width/2, height-ground_height/2-40)
-- tvar a rozměry
objects.ground.shape = love.physics.newRectangleShape(0, 0, width, ground_height, -0.15)
-- propojení tvaru s tělesem
objects.ground.fixture = love.physics.newFixture(objects.ground.body, objects.ground.shape, 5)
objects.ground.fixture:setRestitution(0.7)
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 400, 100, "dynamic")
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(40)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.9)
-- těleso představující druhý míček
objects.ball2 = {}
-- počáteční umístění tělesa
objects.ball2.body = love.physics.newBody(world, 225, 50, "dynamic")
-- tvar a rozměry
objects.ball2.shape = love.physics.newCircleShape(50)
-- propojení tvaru s tělesem
objects.ball2.fixture = love.physics.newFixture(objects.ball2.body, objects.ball2.shape, 5000)
objects.ball2.fixture:setRestitution(0.1)
-- těleso představující kvádr
objects.block3 = {}
-- počáteční umístění tělesa
objects.block3.body = love.physics.newBody(world, 450, 50, "dynamic")
-- tvar a rozměry
objects.block3.shape = love.physics.newRectangleShape(100, 100)
-- propojení tvaru s tělesem
objects.block3.fixture = love.physics.newFixture(objects.block3.body, objects.block3.shape, 5)
objects.block3.fixture:setRestitution(0.0)
end
--
-- Funkce volaná cca 30x za sekundu
--
function love.update(dt)
-- přepočítat parametry celého "světa"
world:update(dt)
local delay = 1/30
if dt < delay then
love.timer.sleep(delay - dt)
end
end
--
-- Tato funkce je volána automaticky při překreslení obsahu
-- okna či obrazovky.
--
function love.draw()
-- vykreslení země
love.graphics.setColor(72, 160, 14)
love.graphics.polygon("line", objects.ground.body:getWorldPoints(objects.ground.shape:getPoints()))
-- vykreslení prvního tělesa (míčku)
love.graphics.setColor(250, 150, 150)
love.graphics.circle("line", objects.ball1.body:getX(), objects.ball1.body:getY(),
objects.ball1.shape:getRadius())
-- vykreslení druhého tělesa (míčku)
love.graphics.setColor(150, 150, 250)
love.graphics.circle("line", objects.ball2.body:getX(), objects.ball2.body:getY(),
objects.ball2.shape:getRadius())
-- vykreslení třetího tělesa (kvádru)
love.graphics.setColor(150, 250, 150)
love.graphics.polygon("line", objects.block3.body:getWorldPoints(objects.block3.shape:getPoints()))
-- výpis zprávy
love.graphics.setColor(250, 250, 250)
love.graphics.print("Escape: to exit.", 20, 615)
end
--
-- Callback funkce zavolaná při stisku klávesy.
--
function love.keypressed(k)
if k == 'escape' then
-- klávesou "Escape" se aplikace ukončí
love.event.quit()
end
end
--
-- finito
--
Obrázek 6: Svět simulovaný v dnešním prvním demonstračním příkladu.
4. Detekce kolizí a obalová tělesa používaná v knihovně LÖVE
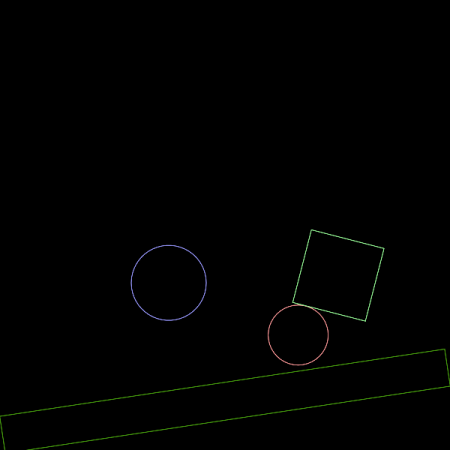
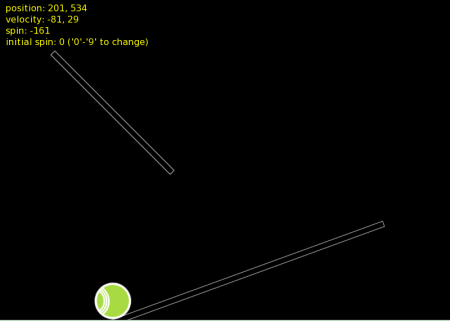
V mnoha aplikacích, především ve hrách, je nutné zaregistrovat okamžik, ve kterém dojde ke kolizi dvou či většího množství těles. Může se například jednat o střet hráče se stěnou, náraz střely do protihráče apod. Engine pak vypočte, jakým způsobem se od sebe tělesa odrazí (připomeňme si, že se stále jedná o nestlačitelná a dokonale neelastická tělesa, takže náraz ani odraz nezmění tvar tělesa). Samotná detekce kolizí je – i když jsou veškeré výpočty prováděny pouze v dvourozměrné ploše – poměrně výpočetně náročná, proto je také množina tvarů, které je možné navázat na tělesa, omezená na výše zmíněné kruhy/kružnice a (uzavřené) konvexní polygony s maximálně osmi hranami. Každý tvar (shape) je navíc vždy uzavřen do takzvaného „obalového tělesa“ (bounding rectangle, obecně bounding box či jen bbox), jehož strany jsou rovnoběžné se souřadnými osami a tudíž je detekce kolizí výrazně jednodušší než v případě obecného polygonu či kruhu. Pokud se totiž neprotínají či ani nedotýkají obalové boxy, nemá smysl provádět složitější výpočet skutečného dotyku těles, což se v praxi ukazuje být velmi významnou optimalizační technikou (dokonce ještě větší význam má v 3D enginech).
Obrázek 7: Obalová tělesa (bounding boxes) zobrazená pro všechny objekty v simulovaném světě.
Obalový obdélník (bounding box) je možné pro libovolný tvar získat metodou Fixture:getBoundingBox(), což si taktéž ukážeme v následujícím demonstračním příkladu. Při každé změně pozice i natočení tvaru je velikost obalového tělesa přepočítána tak, aby tvar vždy ležel uvnitř tohoto tělesa a současně byla jeho plocha minimální (jak bude z animací patrné, tato podmínka není vždy splněna, protože se ještě bere v úvahu vektor rychlosti pohybu tělesa). Jak jsme si již řekli v předchozím odstavci, probíhá detekce kolizí vždy nejprve nad obalovými tělesy a teprve v okamžiku, kdy dojde k jejich prolnutí (či alespoň dotyku) nastává obecně složitější část výpočtu – detekce kolize samotných tvarů. Jen pro úplnost: výše zmíněná metoda Fixture:getBoundingBox() vrací dva protilehlé vrcholy obalového obdélníku. V předchozích verzích knihovny LÖVE existovala i podobně pojmenovaná metoda Shape:getBoundingBox() vracející čtveřici vrcholů (tedy osm souřadnic). Předností této metody byl fakt, že její návratové hodnoty (osm hodnot) bylo možné ihned předat funkci love.draw.polygon() a obalové těleso tak vykreslit na obrazovku.
Obrázek 8: Obalová tělesa (bounding boxes) zobrazená pro všechny objekty v simulovaném světě (i pro polygon).
5. Zdrojový kód druhého demonstračního příkladu
V dnešním druhém demonstračním příkladu je ukázáno, jakým způsobem je možné pro všechny objekty, které se nachází v simulovaném světě, získat a následně zobrazit obalové těleso, a to nezávisle na tom, jaký má objekt tvar. Jediná změna byla provedena v callback funkci love.draw():
--
-- Tato funkce je volána automaticky při překreslení obsahu
-- okna či obrazovky.
--
function love.draw()
...
...
...
-- vykreslení obalových těles
love.graphics.setColor(128, 128, 128)
local x1,y1,x2,y2 = objects.ball1.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
local x1,y1,x2,y2 = objects.ball2.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
local x1,y1,x2,y2 = objects.block3.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
...
...
...
end
Obrázek 9: Povšimněte si, jak se při pohybu obalová tělesa „natahují“ a neodpovídají přímo tvarům objektů.
Úplný zdrojový kód demonstračního příkladu:
--
-- Knihovna LÖVE
--
-- Dvacátý první demonstrační příklad
--
-- Jednoduchý "svět", v němž se nachází dva míčky a jeden kvádr.
-- Při vykreslování scény se zvýrazní i obalová tělesa.
--
-- rozměry okna, do něhož se bude provádět vykreslování
width = 600
height = 600
ground_height = 50
-- tíhové zrychlení
G = 9.81
-- počet pixelů odpovídající jednomu metru v simulovaném světě
pixels_per_meter = 64
--
-- Funkce volaná při inicializaci aplikace.
--
function love.load()
-- načtení standardního fontu a nastavení grafického režimu
local font = love.graphics.newFont(love.default_font, 40)
-- inicializace grafického režimu
love.graphics.setMode(width, height, false, false, 0)
-- nastavení rozměrů simulovaného světa
-- (mapování fyzikálních jednotek na pixely)
love.physics.setMeter(pixels_per_meter)
-- vytvoření simulovaného světa
world = love.physics.newWorld(0, G * pixels_per_meter, true)
-- tabulka s tělesy
objects = {}
-- těleso představující zemi
objects.ground = {}
-- počáteční umístění tělesa
objects.ground.body = love.physics.newBody(world, width/2, height-ground_height/2-40)
-- tvar a rozměry
objects.ground.shape = love.physics.newRectangleShape(0, 0, width, ground_height, -0.07)
-- propojení tvaru s tělesem
objects.ground.fixture = love.physics.newFixture(objects.ground.body, objects.ground.shape, 5)
objects.ground.fixture:setRestitution(0.7)
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 400, 100, "dynamic")
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(40)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.2)
-- těleso představující druhý míček
objects.ball2 = {}
-- počáteční umístění tělesa
objects.ball2.body = love.physics.newBody(world, 260, 10, "dynamic")
-- tvar a rozměry
objects.ball2.shape = love.physics.newCircleShape(50)
-- propojení tvaru s tělesem
objects.ball2.fixture = love.physics.newFixture(objects.ball2.body, objects.ball2.shape, 5000)
objects.ball2.fixture:setRestitution(0.1)
-- těleso představující kvádr
objects.block3 = {}
-- počáteční umístění tělesa
objects.block3.body = love.physics.newBody(world, 400, 20, "dynamic")
-- tvar a rozměry
objects.block3.shape = love.physics.newRectangleShape(150, 10)
-- propojení tvaru s tělesem
objects.block3.fixture = love.physics.newFixture(objects.block3.body, objects.block3.shape, 5)
objects.block3.fixture:setRestitution(0.1)
end
--
-- Funkce volaná cca 30x za sekundu
--
function love.update(dt)
-- přepočítat parametry celého "světa"
world:update(dt)
local delay = 1/30
if dt < delay then
love.timer.sleep(delay - dt)
end
end
--
-- Tato funkce je volána automaticky při překreslení obsahu
-- okna či obrazovky.
--
function love.draw()
-- vykreslení země
love.graphics.setColor(72, 160, 14)
love.graphics.polygon("line", objects.ground.body:getWorldPoints(objects.ground.shape:getPoints()))
-- vykreslení prvního tělesa (míčku)
love.graphics.setColor(250, 150, 150)
love.graphics.circle("line", objects.ball1.body:getX(), objects.ball1.body:getY(),
objects.ball1.shape:getRadius())
-- vykreslení druhého tělesa (míčku)
love.graphics.setColor(150, 150, 250)
love.graphics.circle("line", objects.ball2.body:getX(), objects.ball2.body:getY(),
objects.ball2.shape:getRadius())
-- vykreslení třetího tělesa (kvádru)
love.graphics.setColor(150, 250, 150)
love.graphics.polygon("line", objects.block3.body:getWorldPoints(objects.block3.shape:getPoints()))
-- vykreslení obalových těles
love.graphics.setColor(128, 128, 128)
local x1,y1,x2,y2 = objects.ball1.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
local x1,y1,x2,y2 = objects.ball2.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
local x1,y1,x2,y2 = objects.block3.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
-- výpis zprávy
love.graphics.setColor(250, 250, 250)
love.graphics.print("Escape: to exit.", 20, 615)
end
--
-- Callback funkce zavolaná při stisku klávesy.
--
function love.keypressed(k)
if k == 'escape' then
-- klávesou "Escape" se aplikace ukončí
love.event.quit()
end
end
--
-- finito
--
Obrázek 10: Screenshot z demonstračního příkladu.
Obrázek 11: Povšimněte si, že při kolizi těles dochází k protnutí jejich bounding boxů.
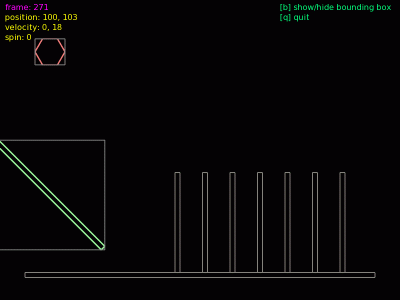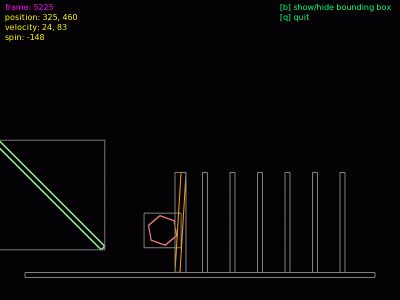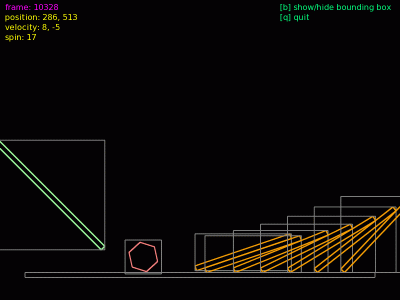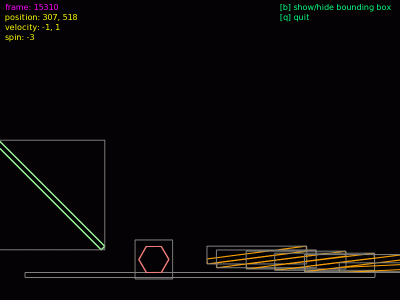
6. Problematika „průstřelu“ tenkých stěn a způsob jejího řešení
Při použití modulu love.physics v simulovaných světech, ve kterých se pohybují objekty vysokou rychlostí a kde se současně nachází úzké stěny, může dojít k případům, kdy kvůli numerickým chybám vzniklým při výpočtu dynamiky těles dojde k nechtěnému „průstřelu“ stěny, tj. těleso je jakoby teleportováno na druhou stranu aniž by došlo k detekci kolize. Aby k tomu problému došlo, musí být splněny dvě tři podmínky:
- Těleso se musí pohybovat poměrně vysokou rychlostí.
- Stěna musí být úzká.
- Navíc musí být stěna taktéž pohyblivá, protože u statických objektů je použit odlišný výpočet kolizí.
Podívejme se nyní na příklad, který problematiku průstřelu ilustruje. Nejprve vytvořme v simulovaném světě úzkou stěnu (její šířka je řízena proměnnou wall_width:
-- těleso představující stěnu
objects.wall = {}
-- počáteční umístění tělesa
objects.wall.body = love.physics.newBody(world, 200, height/2, "dynamic")
-- tvar a rozměry
-- hodnota wall_width bude typicky hodně malá, například 1, 2, 3 jednotky
objects.wall.shape = love.physics.newRectangleShape(wall_width, 200)
-- propojení tvaru s tělesem
objects.wall.fixture = love.physics.newFixture(objects.wall.body, objects.wall.shape, 5)
objects.wall.fixture:setRestitution(0.7)
Následně je do scény přidáno těleso, které se ke stěně rychle přibližuje (v kolmém směru, ale to ve skutečnosti není zcela nezbytné):
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 550, height/2, "dynamic")
-- vysoká počáteční rychlost s vektorem směřujícím doleva
objects.ball1.body:setLinearVelocity(-10000000,0)
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(5)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.2)
Co se nyní stane dobře ilustrují následující tři obrázky, na nichž je taktéž vidět obalové těleso míčku:
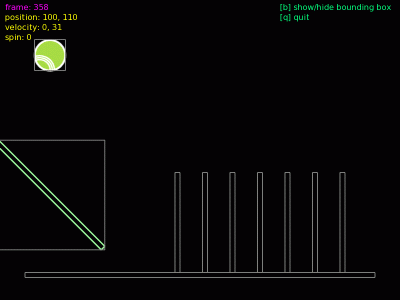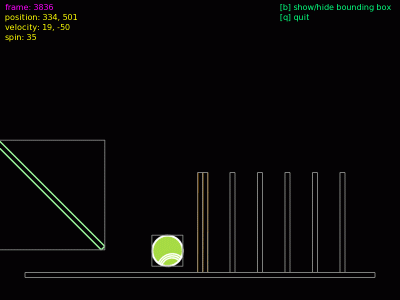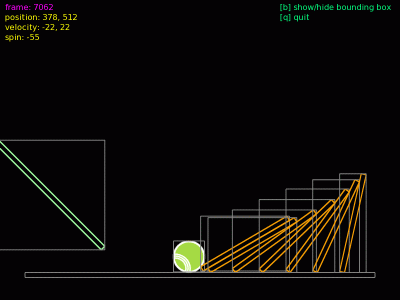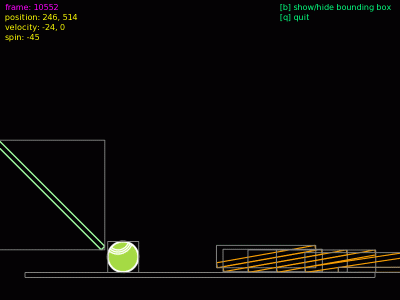
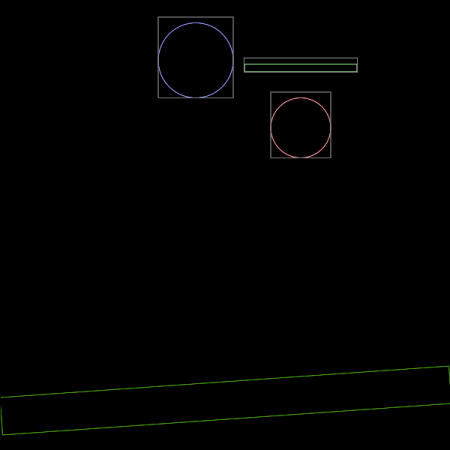
Obrázek 12: Začátek simulace; ve světě se nachází jen podlaha a stěna.
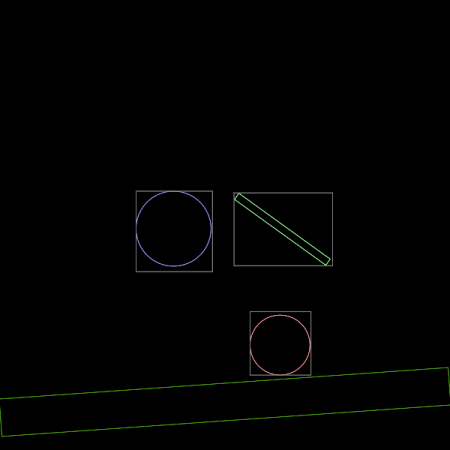
Obrázek 13: Ke stěně se začíná přibližovat rychle se pohybující těleso. Povšimněte si „natažení“ jeho bounding boxu.
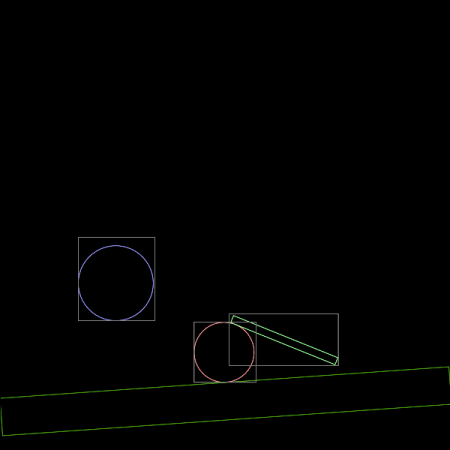
Obrázek 14: Těleso se pohybuje tak rychle, že algoritmus detekce kolize nezareagoval na průstřel (kulička by se měla odrazit).
7. Zdrojový kód třetího demonstračního příkladu
Problematiku průstřelu úzkých stěn si můžeme snadno předvést na dalším (dnes již třetím) demonstračním příkladu. V něm jsou vytvořena pouhá tři tělesa: nehybná podlaha, stěna (ta musí být „dynamická“, aby se použil správný algoritmus detekce kolize) a samotná rychle se pohybující kulička. Po spuštění by mělo dojít k průstřelu, na který ani jedno těleso (stěna, kulička) správně nezareaguje: kulička stěnou prolétne a stěna spadne na podlahu (dokonce se ani nenakloní). Následuje výpis zdrojového kódu dnešního třetího demonstračního příkladu:
--
-- Knihovna LÖVE
--
-- Dvacátý druhý demonstrační příklad
--
-- Jednoduchý "svět", v němž se nachází stěna a rychle se pohybující kulička
-- ("střela").
--
-- rozměry okna, do něhož se bude provádět vykreslování
width = 600
height = 600
-- parametry podlahy a stěny
ground_height = 50
wall_width = 2
-- tíhové zrychlení
G = 9.81
-- počet pixelů odpovídající jednomu metru v simulovaném světě
pixels_per_meter = 64
--
-- Funkce volaná při inicializaci aplikace.
--
function love.load()
-- načtení standardního fontu a nastavení grafického režimu
local font = love.graphics.newFont(love.default_font, 40)
-- inicializace grafického režimu
love.graphics.setMode(width, height, false, false, 0)
-- nastavení rozměrů simulovaného světa
-- (mapování fyzikálních jednotek na pixely)
love.physics.setMeter(pixels_per_meter)
-- vytvoření simulovaného světa
world = love.physics.newWorld(0, G * pixels_per_meter, true)
-- tabulka s tělesy
objects = {}
-- těleso představující zemi
objects.ground = {}
-- počáteční umístění tělesa
objects.ground.body = love.physics.newBody(world, width/2, height-ground_height/2-40)
-- tvar a rozměry
objects.ground.shape = love.physics.newRectangleShape(width, ground_height)
-- propojení tvaru s tělesem
objects.ground.fixture = love.physics.newFixture(objects.ground.body, objects.ground.shape, 5)
objects.ground.fixture:setRestitution(0.7)
-- těleso představující stěnu
objects.wall = {}
-- počáteční umístění tělesa
objects.wall.body = love.physics.newBody(world, 200, height/2, "dynamic")
-- tvar a rozměry
objects.wall.shape = love.physics.newRectangleShape(wall_width, 200)
-- propojení tvaru s tělesem
objects.wall.fixture = love.physics.newFixture(objects.wall.body, objects.wall.shape, 5)
objects.wall.fixture:setRestitution(0.7)
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 550, height/2, "dynamic")
objects.ball1.body:setLinearVelocity(-10000000,0)
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(5)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.2)
end
--
-- Funkce volaná cca 30x za sekundu
--
function love.update(dt)
-- přepočítat parametry celého "světa"
world:update(dt)
local delay = 1/30
if dt < delay then
love.timer.sleep(delay - dt)
end
end
--
-- Tato funkce je volána automaticky při překreslení obsahu
-- okna či obrazovky.
--
function love.draw()
-- vykreslení země
love.graphics.setColor(72, 160, 14)
love.graphics.polygon("line", objects.ground.body:getWorldPoints(objects.ground.shape:getPoints()))
-- vykreslení stěny
love.graphics.setColor(250, 100, 100)
love.graphics.polygon("line", objects.wall.body:getWorldPoints(objects.wall.shape:getPoints()))
-- vykreslení míčku
love.graphics.setColor(250, 250, 150)
love.graphics.circle("line", objects.ball1.body:getX(), objects.ball1.body:getY(),
objects.ball1.shape:getRadius())
-- vykreslení obalových těles
love.graphics.setColor(128, 128, 128)
local x1,y1,x2,y2 = objects.ball1.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
-- výpis zprávy
love.graphics.setColor(250, 250, 250)
love.graphics.print("Escape: to exit.", 20, 615)
end
--
-- Callback funkce zavolaná při stisku klávesy.
--
function love.keypressed(k)
if k == 'escape' then
-- klávesou "Escape" se aplikace ukončí
love.event.quit()
end
end
--
-- finito
--
Obrázek 15: Namísto přímého vykreslení tvarů s využitím úseček, polyčar, kružnic a polygonů lze použít i sprity.
8. Použití přesnějšího výpočtu kolizí
V enginu používaném modulem love.physics je možné provést výběr algoritmu pro výpočet kolizí. Pro statická tělesa (která se nepohybují) je implementován přesnější a současně i pomalejší výpočet, pro dynamická tělesa (která se naopak pohybují) pak výpočet rychlejší, ovšem s výše zmíněnou nepřesností. Pokud však programátor ví, že se v jeho simulovaném světě budou nacházet rychle se pohybující tělesa a úzké stěny, může algoritmus detekce kolizí pro vybraná tělesa jednoduše přepnout, a to konkrétně metodou Body:setBullet(). Této metodě se předává pravdivostní hodnota true či false podle toho, zda má být dané těleso považováno za „střelu“, tj. rychle se pohybující předmět či za běžné pomaleji se pohybující těleso.
V praxi se celá simulace při přepnutí míčku do režimu „střely“ bude diametrálně odlišovat. Opět se podívejme na čtyři ilustrační obrázky, kde se míček/střela pohybuje velkou rychlostí proti úzké stěně:
Obrázek 16: Začátek simulace; ve světě se prozatím nachází jen podlaha a stěna.
Obrázek 17: Ke stěně se začíná přibližovat rychle se pohybující těleso (střela). Opět si povšimněte „natažení“ jeho bounding boxu.
Obrázek 18: Došlo ke kolizi a odrazu těles – stěna se posunula směrem doleva, kulička se odrazila doprava a ztratila část své rychlosti (vektor rychlosti se současně otočil).
Obrázek 19: Jak na stěnu, tak i na kuličku začíná výrazněji působit gravitace.
9. Zdrojový kód čtvrtého demonstračního příkladu
Přepnutí algoritmu pro výpočet kolizí na jeho přesnější a současně i pomalejší variantu je jednoduché, což je ostatně patrné i z následujícího úryvku zdrojového kódu, v němž je příslušný programový řádek zvýrazněn. Povšimněte si, že volbu algoritmu je možné provést pro každé těleso zvlášť, takže závisí jen a pouze na vývojáři, ve kterých případech bude preferovat rychlejší výpočet a kdy naopak výpočet přesnější:
--
-- Funkce volaná při inicializaci aplikace.
--
function love.load()
...
...
...
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 550, height/2, "dynamic")
objects.ball1.body:setLinearVelocity(-10000000,0)
-- nutno nastavit na "true" - použije se pomalejší ale přesnější algoritmus výpočtu
objects.ball1.body:setBullet(true)
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(5)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.2)
...
...
...
end
Podívejme se nyní na výpis zdrojového kódu dnešního čtvrtého demonstračního příkladu:
--
-- Knihovna LÖVE
--
-- Dvacátý třetí demonstrační příklad
--
-- Vyřešení problémů s rychle se pohybujícími tělesy
--
-- rozměry okna, do něhož se bude provádět vykreslování
width = 600
height = 600
-- parametry podlahy a stěny
ground_height = 50
wall_width = 2
-- tíhové zrychlení
G = 9.81
-- počet pixelů odpovídající jednomu metru v simulovaném světě
pixels_per_meter = 64
--
-- Funkce volaná při inicializaci aplikace.
--
function love.load()
-- načtení standardního fontu a nastavení grafického režimu
local font = love.graphics.newFont(love.default_font, 40)
-- inicializace grafického režimu
love.graphics.setMode(width, height, false, false, 0)
-- nastavení rozměrů simulovaného světa
-- (mapování fyzikálních jednotek na pixely)
love.physics.setMeter(pixels_per_meter)
-- vytvoření simulovaného světa
world = love.physics.newWorld(0, G * pixels_per_meter, true)
-- tabulka s tělesy
objects = {}
-- těleso představující zemi
objects.ground = {}
-- počáteční umístění tělesa
objects.ground.body = love.physics.newBody(world, width/2, height-ground_height/2-40)
-- tvar a rozměry
objects.ground.shape = love.physics.newRectangleShape(width, ground_height)
-- propojení tvaru s tělesem
objects.ground.fixture = love.physics.newFixture(objects.ground.body, objects.ground.shape, 5)
objects.ground.fixture:setRestitution(0.7)
-- těleso představující stěnu
objects.wall = {}
-- počáteční umístění tělesa
objects.wall.body = love.physics.newBody(world, 200, height/2, "dynamic")
-- tvar a rozměry
objects.wall.shape = love.physics.newRectangleShape(wall_width, 200)
-- propojení tvaru s tělesem
objects.wall.fixture = love.physics.newFixture(objects.wall.body, objects.wall.shape, 5)
objects.wall.fixture:setRestitution(0.7)
-- těleso představující první míček
objects.ball1 = {}
-- počáteční umístění tělesa
objects.ball1.body = love.physics.newBody(world, 550, height/2, "dynamic")
objects.ball1.body:setLinearVelocity(-10000000,0)
-- nutno nastavit na "true" - použije se pomalejší ale přesnější algoritmus výpočtu
objects.ball1.body:setBullet(true)
-- tvar a rozměry
objects.ball1.shape = love.physics.newCircleShape(5)
-- propojení tvaru s tělesem
objects.ball1.fixture = love.physics.newFixture(objects.ball1.body, objects.ball1.shape, 5)
objects.ball1.fixture:setRestitution(0.2)
end
--
-- Funkce volaná cca 30x za sekundu
--
function love.update(dt)
-- přepočítat parametry celého "světa"
world:update(dt)
local delay = 1/30
if dt < delay then
love.timer.sleep(delay - dt)
end
end
--
-- Tato funkce je volána automaticky při překreslení obsahu
-- okna či obrazovky.
--
function love.draw()
-- vykreslení země
love.graphics.setColor(72, 160, 14)
love.graphics.polygon("line", objects.ground.body:getWorldPoints(objects.ground.shape:getPoints()))
-- vykreslení stěny
love.graphics.setColor(250, 100, 100)
love.graphics.polygon("line", objects.wall.body:getWorldPoints(objects.wall.shape:getPoints()))
-- vykreslení míčku
love.graphics.setColor(250, 250, 150)
love.graphics.circle("line", objects.ball1.body:getX(), objects.ball1.body:getY(),
objects.ball1.shape:getRadius())
-- vykreslení obalových těles
love.graphics.setColor(128, 128, 128)
local x1,y1,x2,y2 = objects.ball1.fixture:getBoundingBox()
love.graphics.rectangle("line", x1, y1, x2-x1, y2-y1)
-- výpis zprávy
love.graphics.setColor(250, 250, 250)
love.graphics.print("Escape: to exit.", 20, 615)
end
--
-- Callback funkce zavolaná při stisku klávesy.
--
function love.keypressed(k)
if k == 'escape' then
-- klávesou "Escape" se aplikace ukončí
love.event.quit()
end
end
--
-- finito
--
Obrázek 20: V příští části miniseriálu o modulu love.physics si ukážeme způsob vzájemného propojení těles různými vazbami.
10. Repositář se zdrojovými kódy všech čtyř dnešních demonstračních příkladů
Všechny čtyři demonstrační příklady, s nimiž jsme se v dnešním článku seznámili, byly uloženy do Git repositáře umístěného na GitHubu (https://github.com/tisnik/presentations). Každý demonstrační příklad je, podobně jako tomu bylo i u obou příkladů z předchozího článku, tvořen pouze zdrojovým kódem uloženým v souboru main.lua:
| # | Příklad | Zdrojový kód |
|---|---|---|
| 1 | example20 | https://github.com/tisnik/presentations/tree/master/love/example20 |
| 2 | example21 | https://github.com/tisnik/presentations/tree/master/love/example21 |
| 3 | example22 | https://github.com/tisnik/presentations/tree/master/love/example22 |
| 4 | example23 | https://github.com/tisnik/presentations/tree/master/love/example23 |
Poznámka: demonstrační příklady jsou číslovány průběžně, protože tento článek (alespoň nepřímo) navazuje na seriál o programovacích jazycích vhodných pro výuku počítačové grafiky.
11. Odkazy na Internetu
- Bounding Boxes
http://www.3dkingdoms.com/weekly/weekly.php?a=21 - Box2D (stránka projektu)
http://box2d.org/ - Box2D FAQ
https://github.com/erincatto/Box2D/wiki/FAQ - Box2D v2.2.0 User Manual
http://www.box2d.org/manual.html - Bounding Box (OpenStreetMap)
http://wiki.openstreetmap.org/wiki/Bounding_Box - Minimum Bounding Rectange (Wikipedia)
https://en.wikipedia.org/wiki/Minimum_bounding_rectangle - Minimum bounding box (Wikipedia)
https://en.wikipedia.org/wiki/Minimum_bounding_box - 2D Bounding Box Collision Detection
http://www.dreamincode.net/forums/topic/180069-xna-2d-bounding-box-collision-detection/ - Chipmunk2D (další fyzikální engine)
http://chipmunk-physics.net/ - Physics Engine (Wikipedia)
https://en.wikipedia.org/wiki/Physics_engine - Modul love.physics
https://love2d.org/wiki/love.physics - Modul love.physics: Objekt typu World
https://love2d.org/wiki/World - Modul love.physics: Objekt typu Body
https://love2d.org/wiki/Body - Modul love.physics: Objekt typu Shape
https://love2d.org/wiki/Shape - Modul love.physics: Objekt typu Joint
https://love2d.org/wiki/Joint - Modul love.physics: Objekt typu Fixture
https://love2d.org/wiki/Fixture - Particle Systems From the Ground Up
http://buildnewgames.com/particle-systems/ - Particle Systems
http://natureofcode.com/book/chapter-4-particle-systems/ - Domovská stránka systému LÖVE
http://love2d.org/ - Dokumentace k systému LÖVE
http://love2d.org/wiki/love - Domovská stránka programovacího jazyka Lua
http://www.lua.org/ - Seriál o programovacím jazyku Lua (root.cz):
http://www.root.cz/serialy/programovaci-jazyk-lua/ - Domovská stránka systému LÖVE
http://love2d.org/ - Domovská stránka programovacího jazyka Lua
http://www.lua.org/ - Web o Lieru, Gusanos, GeneRally, Atari atd.
http://karelik.wz.cz/ - Web o Lieru, Gusanos
http://karelik.wz.cz/gusanos.php - GUSANOS
http://gusanos.sourceforge.net/ - GUSANOS Download
http://sourceforge.net/projects/gusanos/ - Lua
http://www.linuxexpres.cz/praxe/lua - Lua
http://cs.wikipedia.org/wiki/Lua - Lua (programming language)
http://en.wikipedia.org/wiki/Lua_(programming_language) - The Lua Programming Language
http://www.tiobe.com/index.php/paperinfo/tpci/Lua.html - Lua Programming Gems
http://www.lua.org/gems/ - LuaForge
http://luaforge.net/ - Forge project tree
http://luaforge.net/softwaremap/trove_list.php - SdlBasic home page
http://www.sdlbasic.altervista.org/main/ - SdlBasic examples
http://nitrofurano.linuxkafe.com/sdlbasic/ - SdlBasic na Wikipedii
http://en.wikipedia.org/wiki/SdlBasic - Simple DirectMedia Layer
http://en.wikipedia.org/wiki/Simple_DirectMedia_Layer - SDLBASIC – The high-level interpreter for all?
http://openbytes.wordpress.com/2008/11/08/sdlbasic-the-high-level-interpreter-for-all/ - FreeBasic home page
http://www.freebasic.net/ - FreeBASIC (Wikipedia EN)
https://en.wikipedia.org/wiki/FreeBASIC - FreeBASIC Wiki
http://www.freebasic.net/wiki/wikka.php?wakka=FBWiki - FreeBASIC Manual
http://www.freebasic.net/wiki/wikka.php?wakka=DocToc - FreeBASIC (Wikipedia CZ)
http://cs.wikipedia.org/wiki/FreeBASIC - The Griffon Legend
http://syn9.thingie.net/?table=griffonlegend - Seriál Letní škola programovacího jazyka Logo
http://www.root.cz/serialy/letni-skola-programovaciho-jazyka-logo/ - Scratch: oficiální stránka projektu
http://scratch.mit.edu/ - Scratch: galerie projektů vytvořených ve Scratchi
http://scratch.mit.edu/galleries/browse/newest - Scratch: nápověda
file:///usr/share/scratch/Help/en/index.html - Scratch: obrazovky nápovědy
file:///usr/share/scratch/Help/en/allscreens.html - Scratch (Wikipedie CZ)
http://cs.wikipedia.org/wiki/Scratch - Scratch (programming language)
http://en.wikipedia.org/wiki/Scratch_(programming_language) - Scratch Modification
http://wiki.scratch.mit.edu/wiki/Scratch_Modification - Scratch Lowers Resistance to Programming
http://www.wired.com/gadgetlab/2009/03/scratch-lowers/ - Snap!
http://snap.berkeley.edu/ - Prostředí Snap!
http://snap.berkeley.edu/snapsource/snap.html - Alternatives to Scratch
http://wiki.scratch.mit.edu/wiki/Alternatives_to_Scratch - Basic-256 home page
http://www.basic256.org/index_en - Basic-256 Language Documentation
http://doc.basic256.org/doku.php - Basic-256 Art Gallery
http://www.basic256.org/artgallery - Basic-256 Tutorial
http://www.basic256.org/tutorials - Why BASIC?
http://www.basic256.org/whybasic - A book to teach ANYBODY how to program a computer (using BASIC)
http://www.basicbook.org/ - BASIC Computer Games (published 1978) - Hammurabi
http://atariarchives.org/basicgames/showpage.php?page=78 - Hamurabi - zdrojový kód v BASICu
http://www.dunnington.u-net.com/public/basicgames/HMRABI