Ve druhém článku věnovaném IPython Notebooku a taktéž knihovně Numpy dokončíme popis základního modulu této knihovny. Nejdříve si vysvětlíme několik principů indexování prvků polí a následně se budeme zabývat vybranými operacemi s maticemi, které jsou v knihovně Numpy dostupné. Nezapomeneme ani na popis některých užitečných funkcí dostupných v submodulu numpy.linalg – výpočet determinantu, výpočet inverzní matice či vyřešení systému lineárních rovnic.
Obsah
2. Indexování prvků polí obsahem jiného pole
4. Použití „kroku“ při provádění řezu polem
6. Výběr prvků pole na základě zadané podmínky
7. Matematické funkce aplikovatelné na prvky polí
8. Sčítání, odčítání a násobení matic
9. Výpočet determinantu a výpočet inverzní matice
10. Vyřešení systému lineárních rovnic
1. Indexování prvků polí
V předchozí části seriálu o vývojových prostředích, která jsou dostupná všem programátorům využívajícím distribuci Fedora, jsme si vysvětlili základní koncepty knihovny Numpy, jež se stala velmi populární, a to nejenom mezi profesionálními vývojáři, ale také mezi amatérskými programátory. Připomeňme si pouze, že tato knihovna je postavena na zpracování polí, ovšem nejedná se o datové struktury spravované přímo interpretrem programovacího jazyka Python (tedy vlastně o seznamy seznamů), ale o skutečně homogenní datové struktury vytvářené a zpřístupněné přes nativní (binární) knihovny. Díky tomuto konceptu bylo možné dosáhnout snížení paměťových nároků a především pak zrychlit přístup k prvkům polí. Navíc je možné provádět změnu tvaru (shape) polí, a to bez nutnosti fyzického přesunu jednotlivých prvků. Tvar pole je tak vlastně jen „pohledem“ (view) na fyzické pole uložené buď v operační paměti počítače či na disku.
Jakým způsobem se pole s využitím knihovny Numpy vytváří již víme. Ještě si však musíme říct, jak se prvky uložené v polích vybírají neboli indexují. V případě jednorozměrných polí je to ve skutečnosti velmi jednoduché – prvky jsou totiž číslovány od nuly a díky přetížení operátoru [] (operátor indexování) je možné prvky v případě potřeby indexovat i od konce pole. V tomto případě se musí použít záporné číslo, takže a[1] značí druhý prvek pole zatímco a[-1] první prvek od konce:
a=numpy.arange(12) a array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) a[0] 0 a[5] 5 a[-1] 11 a[-5] 7
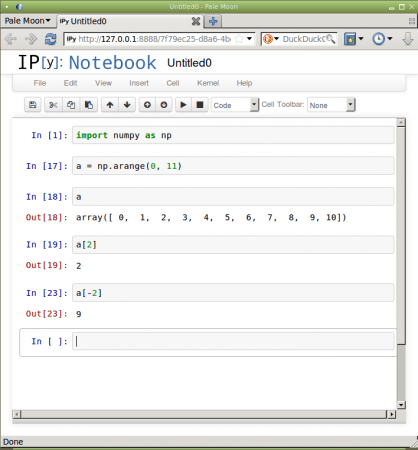
Obrázek 1: Indexování prvků v jednorozměrných polích.
U dvourozměrných či vícerozměrných polí je situace poněkud komplikovanější, neboť v tomto případě je nutné použít dva či větší počet indexů (jeden index pro každou dimenzi). Vzhledem k tomu, že v různých programovacích jazycích a rozličných specializovaných nástrojích typu R či Matlab, se používají odlišné způsoby zápisu více indexů, podporuje knihovna Numpy dva způsoby zápisu – buď se všechny indexy oddělí čárkou a vloží se do jediného bloku omezeného hranatými závorkami [], nebo se alternativně pro každou dimenzi použije zvláštní hranatá závorka (syntaxe odvozená od Céčka):
import numpy
m=numpy.reshape(numpy.arange(12), (3,4))
m
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
m[0]
array([0, 1, 2, 3])
m[0][2]
2
m[0,2]
2
2. Indexování prvků polí obsahem jiného pole
Třetí možností, jak získat část prvků z nějakého pole, spočívá v indexování prvků tohoto pole jiným polem. To je velmi zajímavá a v mnoha operacích užitečná alternativa, takže se podívejme, jak ji je možné použít v praxi. Pole b, resp. jeho obsah slouží pro indexování pole a:
a=numpy.arange(12) a array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19]) b=numpy.array([1,2,9,8,5]) a[b] array([11, 12, 19, 18, 15]) b=numpy.array([1,2,-1,8,5]) a[b] array([11, 12, 19, 18, 15])
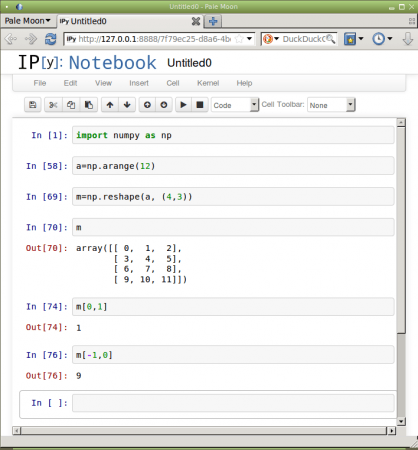
Obrázek 2: Indexování prvků ve dvourozměrném poli.
Zkusme stejnou operaci provést s dvourozměrným polem:
m1=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
m1
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
m2=numpy.array([0,2,1])
m1[m2]
array([[1, 2, 3],
[7, 8, 9],
[4, 5, 6]])
3. Vytváření „řezů“ z polí
V mnoha případech je nutné z polí získat hodnoty většího množství prvků tvořících souvislý blok. Může se například jednat o všechny prvky pole kromě prvku prvního a posledního (typické pro některé filtry), prvky z první poloviny pole atd. I v tomto případě knihovna Numpy nabízí vývojářům velmi elegantní řešení, a to ve formě takzvaných řezů (slices). Namísto jediného indexu je totiž možné zadat dva indexy oddělené dvojtečkou, které potom reprezentují začátek a konec řezu. Opět se podívejme na demonstrační příklad:
a=numpy.arange(12) a array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) a[3:7] array([3, 4, 5, 6])
Pokud se vynechá první index, automaticky se za něj dosadí 0, pokud se vynechá index druhý, dosadí se za něj velikost dimenze pole-1. Vynechat je možné i oba indexy; v tomto případě je řezem původní pole (tento zápis je sice možný, ale poněkud postrádá smysl):
a=numpy.arange(12) a[:7] array([0, 1, 2, 3, 4, 5, 6]) a[5:] array([ 5, 6, 7, 8, 9, 10, 11]) a[:] array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
Někdy může být řez polem prázdný:
a=numpy.arange(12) a array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) a[-4:-6] array([], dtype=int64)
Použít je možné i záporné indexy popř. první či druhý index zcela vynechat:
a[-6:-4] array([6, 7]) a[-6:] array([ 6, 7, 8, 9, 10, 11]) a[:-4] array([0, 1, 2, 3, 4, 5, 6, 7])
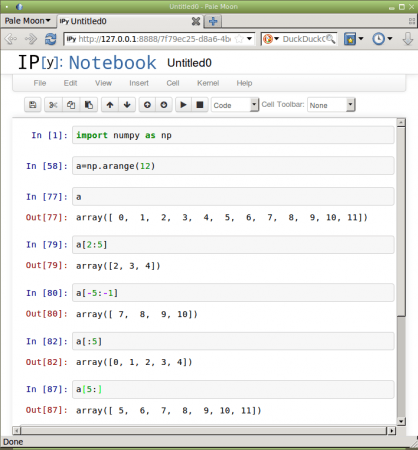
Obrázek 3: Řezy jednorozměrným polem.
Řezy je možné provádět i u dvourozměrných či vícerozměrných polí. V tomto případě se zkombinuje zápis popsaný v první kapitole s dvojtečkou:
import numpy
m=numpy.reshape(numpy.arange(25), (5,5))
m
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
array([[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
m[2:4,3]
array([13, 18])
m[2:4,3:5]
array([[13, 14],
[18, 19]])
m[1:4,1:4]
array([[ 6, 7, 8],
[11, 12, 13],
[16, 17, 18]])
m[-4:-2,-4:-2]
array([[ 6, 7],
[11, 12]])
4. Použití „kroku“ při provádění řezu polem
Při provádění operace řezu polem jsme doposud používali zápis pole[i1:i2], popř. se jeden z indexů i1 či i2 mohl vynechat. Ovšem knihovna Numpy podporuje ještě zápis pole[i1:i2:step], přičemž poslední použitá hodnota udává vzdálenost mezi sousedními prvky řezu. Podívejme se na příklad:
a=numpy.arange(1,11) a array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) a[1:10:1] array([ 2, 3, 4, 5, 6, 7, 8, 9, 10]) a[1:10:2] array([ 2, 4, 6, 8, 10]) a[1:10:3] array([2, 5, 8]) a[::3] array([ 1, 4, 7, 10])
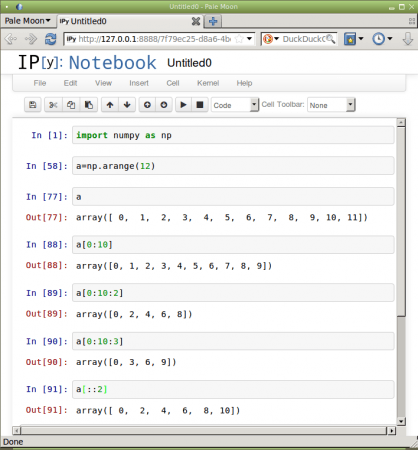
Obrázek 4: Řezy jednorozměrným polem s udáním kroku.
Samozřejmě je možné prakticky tutéž operaci provést i u dvourozměrných polí:
m1=numpy.reshape(numpy.arange(0,25), (5,5))
m1
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
m1[0:5:2]
array([[ 0, 1, 2, 3, 4],
[10, 11, 12, 13, 14],
[20, 21, 22, 23, 24]])
m1[1::2]
array([[ 5, 6, 7, 8, 9],
[15, 16, 17, 18, 19]])
Či dokonce takto (sudé sloupce a sudé řádky):
m1[::2,::2]
array([[ 0, 2, 4],
[10, 12, 14],
[20, 22, 24]])
5. Pole a relační operátory
V případě importu knihovny Numpy dojde k přetížení mnoha dalších operátorů. Jedná se zejména o relační operátory, tj. o takové operátory, které slouží k porovnání dvou hodnot. Ve svém původním významu tyto operátory vrací jedinou pravdivostní hodnotu True nebo False. Ovšem pokud se relační operátory použijí ve své přetížené variantě pro porovnání polí (vektorů, matic), je výsledkem opět pole, ovšem pouze s hodnotami True a False vzniklými porovnáním prvků polí se stejným indexem. Při porovnávání musí mít obě pole stejný tvar, což je kontrolováno za běhu aplikace:
a=numpy.arange(1,11) b=numpy.array([100,0,100,0,100,0,100,0,100,0]) a array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) b array([100, 0, 100, 0, 100, 0, 100, 0, 100, 0]) a==b array([False, False, False, False, False, False, False, False, False, False], dtype=bool) a!=b array([ True, True, True, True, True, True, True, True, True, True], dtype=bool) a<b array([ True, False, True, False, True, False, True, False, True, False], dtype=bool)
Relační operátory je možné použít i tak, že jedním z operandů je pole a druhým operandem je skalární hodnota. Výsledkem takového porovnání je opět pole, tentokrát vytvořené porovnáním každého prvku zdrojového pole s jedinou skalární hodnotou:
a=numpy.arange(12)
a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
a==5
array([False, False, False, False, True, False, False, False, False, False], dtype=bool)
a<6
array([ True, True, True, True, True, True, False, False, False,
False, False, False], dtype=bool)
Podobně můžeme vytvořit „Booleovská“ dvourozměrná pole:
m=numpy.arange(24)
m
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])
x=numpy.reshape(m, (6,4), order='F')
x>10
array([[False, False, True, True],
[False, False, True, True],
[False, False, True, True],
[False, False, True, True],
[False, False, True, True],
[False, True, True, True]], dtype=bool)
x%2==1
array([[False, False, False, False],
[ True, True, True, True],
[False, False, False, False],
[ True, True, True, True],
[False, False, False, False],
[ True, True, True, True]], dtype=bool)
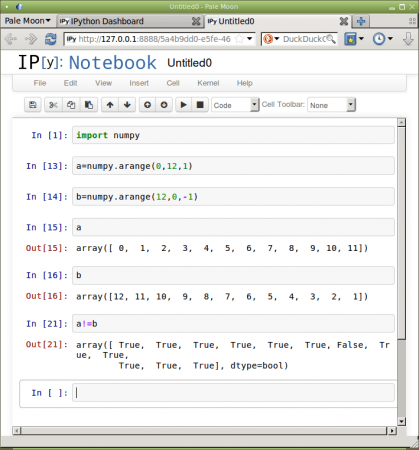
Obrázek 5: Porovnání dvojice jednorozměrných polí (vektorů).
6. Výběr prvků pole na základě zadané podmínky
K čemu však mohou být pole, která jsou výsledkem aplikace přetížených relačních operátorů, užitečná v praxi? Knihovna Numpy svým uživatelům ve skutečnosti nabízí ještě jednu důležitou metodu výběru prvků z polí. Jedná se o takzvanou filtraci, kdy se pro výběr prvku z jednoho pole použije jiné pole obsahující pouze pravdivostní hodnoty. V takovém případě se vrátí nové pole, ovšem pouze s těmi prvky, pro které platí pole2[index]==True. Podívejme se na typický demonstrační příklad:
a=numpy.arange(12)
a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
a<6
array([ True, True, True, True, True, True, False, False, False,
False, False, False], dtype=bool)
Nyní na řadu přichází zmíněný trik: nové pole (které ovšem není uloženo do žádné proměnné) vytvořené operací a<6, se použije pro „filtraci“ původního pole:
a[a<6] array([0, 1, 2, 3, 4, 5])
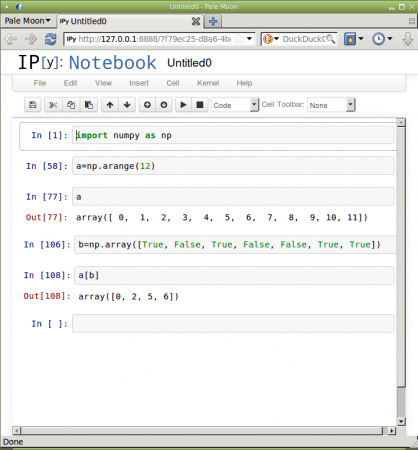
Obrázek 6: Výběr prvků na základě „Boolovského“ pole.
Podobně můžeme z pole získat jen sudé prvky:
a[a%2 == 0] array([ 0, 2, 4, 6, 8, 10])
U dvourozměrných či vícerozměrných polí je situace poněkud složitější, protože výsledkem filtrace je jednorozměrné pole s vybranými (filtrovanými) prvky. Ostatně se o tom můžeme snadno přesvědčit:
m1=numpy.reshape(numpy.arange(100,125),(5,5))
m1
array([[100, 101, 102, 103, 104],
[105, 106, 107, 108, 109],
[110, 111, 112, 113, 114],
[115, 116, 117, 118, 119],
[120, 121, 122, 123, 124]])
m1[m1%2 == 0]
array([100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120, 122, 124])
Popř. pro pole se třemi dimenzemi:
d3=numpy.reshape(numpy.arange(0,27), (3,3,3))
d3
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
d3[d3%3 == 1]
array([ 1, 4, 7, 10, 13, 16, 19, 22, 25])
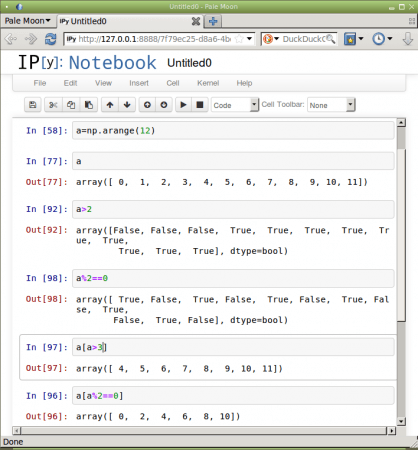
Obrázek 7: Pole a relační operátory.
7. Matematické funkce aplikovatelné na prvky polí
Vzhledem k tomu, že pro práci s poli byly přetíženy relační operátory, asi nás příliš nepřekvapí, že přetíženy byly i běžné aritmetické operátory. V knihovně Numpy není prakticky nic jednoduššího, než přičíst nějakou skalární hodnotu ke všem prvkům pole (resp. přesněji řečeno matice o rozměrech 5×5 prvků):
m=numpy.reshape(numpy.arange(25),(5,5))
m-10
array([[-10, -9, -8, -7, -6],
[ -5, -4, -3, -2, -1],
[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14]])
Podobným způsobem lze použít i další aritmetické operace:
m*2
array([[ 0, 2, 4, 6, 8],
[10, 12, 14, 16, 18],
[20, 22, 24, 26, 28],
[30, 32, 34, 36, 38],
[40, 42, 44, 46, 48]])
m%2
array([[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0]])
Kromě toho v knihovně Numpy nalezneme i množství běžných matematických (zejména goniometrických) funkcí upravených takovým způsobem, aby tyto funkce byly aplikovatelné na pole. Přesný popis těchto funkcí naleznete na stránce http://docs.scipy.org/doc/numpy/reference/routines.math.html:
numpy.abs(m-10)
array([[10, 9, 8, 7, 6],
[ 5, 4, 3, 2, 1],
[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
Příklad použití goniometrické funkce sinus:
a=numpy.linspace(0, numpy.pi/2)
a
array([ 0. , 0.03205707, 0.06411414, 0.0961712 , 0.12822827,
0.16028534, 0.19234241, 0.22439948, 0.25645654, 0.28851361,
0.32057068, 0.35262775, 0.38468481, 0.41674188, 0.44879895,
0.48085602, 0.51291309, 0.54497015, 0.57702722, 0.60908429,
0.64114136, 0.67319843, 0.70525549, 0.73731256, 0.76936963,
0.8014267 , 0.83348377, 0.86554083, 0.8975979 , 0.92965497,
0.96171204, 0.9937691 , 1.02582617, 1.05788324, 1.08994031,
1.12199738, 1.15405444, 1.18611151, 1.21816858, 1.25022565,
1.28228272, 1.31433978, 1.34639685, 1.37845392, 1.41051099,
1.44256806, 1.47462512, 1.50668219, 1.53873926, 1.57079633])
numpy.sin(a)
array([ 0. , 0.03205158, 0.06407022, 0.09602303, 0.12787716,
0.1595999 , 0.19115863, 0.22252093, 0.25365458, 0.28452759,
0.31510822, 0.34536505, 0.375267 , 0.40478334, 0.43388374,
0.46253829, 0.49071755, 0.51839257, 0.5455349 , 0.57211666,
0.59811053, 0.6234898 , 0.6482284 , 0.67230089, 0.69568255,
0.71834935, 0.740278 , 0.76144596, 0.78183148, 0.80141362,
0.82017225, 0.8380881 , 0.85514276, 0.8713187 , 0.88659931,
0.90096887, 0.91441262, 0.92691676, 0.93846842, 0.94905575,
0.95866785, 0.96729486, 0.97492791, 0.98155916, 0.98718178,
0.99179001, 0.99537911, 0.99794539, 0.99948622, 1. ])
8. Sčítání, odčítání a násobení matic
V případě, že uživatel vytvoří matice o stejné velikosti, lze takové matice sčítat či odčítat. Pokud se k matici přičte či odečte skalární hodnota (matice+10, matice-42), jedná se o operaci prováděnou s každým prvkem matice zvlášť (sčítají se prvky se shodným indexem či indexy):
m1=numpy.reshape(numpy.arange(25), (5,5))
m1
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
m2=m1-10
m2
array([[-10, -9, -8, -7, -6],
[ -5, -4, -3, -2, -1],
[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[ 10, 11, 12, 13, 14]])
Zajímavá situace nastane ve chvíli, kdy použijeme operátor *, tedy násobení. Nejprve se podívejme, jaký získáme výsledek při aplikaci „obyčejného“ operátoru *:
m1*m1
array([[ 0, 1, 4, 9, 16],
[ 25, 36, 49, 64, 81],
[100, 121, 144, 169, 196],
[225, 256, 289, 324, 361],
[400, 441, 484, 529, 576]])
m1*m2
array([[ 0, -9, -16, -21, -24],
[-25, -24, -21, -16, -9],
[ 0, 11, 24, 39, 56],
[ 75, 96, 119, 144, 171],
[200, 231, 264, 299, 336]])
Vidíme, že operátor * aplikovaný na matice ve skutečnosti vynásobil vždy příslušné prvky se shodnými indexy, chová se tedy podobně, jako operátory + a - (samozřejmě se provádí odlišná operace, ale princip výběru prvků zůstává stejný). Pokud budeme chtít provést skutečný maticový součin, je nutné namísto prosté aplikace operátoru * zavolat funkci numpy.dot(matice1, matice2):
numpy.dot(m1,m1)
array([[ 150, 160, 170, 180, 190],
[ 400, 435, 470, 505, 540],
[ 650, 710, 770, 830, 890],
[ 900, 985, 1070, 1155, 1240],
[1150, 1260, 1370, 1480, 1590]])
numpy.dot(m1,m2)
array([[ 50, 60, 70, 80, 90],
[ 50, 85, 120, 155, 190],
[ 50, 110, 170, 230, 290],
[ 50, 135, 220, 305, 390],
[ 50, 160, 270, 380, 490]])
numpy.dot(m2,m1)
array([[-350, -390, -430, -470, -510],
[-100, -115, -130, -145, -160],
[ 150, 160, 170, 180, 190],
[ 400, 435, 470, 505, 540],
[ 650, 710, 770, 830, 890]])
Lepší bude si tuto operaci otestovat na menších maticích:
m1=numpy.array([[1,0],[0,1]])
m2=numpy.array([[1,2],[3,4]])
numpy.dot(m2,m1)
array([[1, 2],
[3, 4]])
m3=numpy.array([[2,0],[0,1]])
numpy.dot(m2,m3)
array([[2, 2],
[6, 4]])
numpy.dot(m3,m3)
array([[4, 0],
[0, 1]])
9. Výpočet determinantu a výpočet inverzní matice
Často prováděnou maticovou operací je výpočet determinantu. Pro tento (ale samozřejmě nejenom pouze pro tento) účel byl do knihovny Numpy přidán submodul nazvaný Numpy.linalg, který je zapotřebí importovat samostatně:
import numpy import numpy.linalg
Po úspěšném importu mají uživatelé k dispozici funkci nazvanou numpy.linalg.det, kterou je možné použít pro výpočet determinantu:
m=numpy.array([[0,1,0],[1,1,1],[0,1,1]])
m
array([[0, 1, 0],
[1, 1, 1],
[0, 1, 1]])
numpy.linalg.det(m)
-1.0
Další užitečnou funkcí, kterou v tomto submodulu nalezneme, je funkce pro výpočet inverzní matice. Tato funkce se jmenuje numpy.linalg.inv a její použití je snadné:
m=numpy.array([[0,1,0],[1,1,1],[0,1,1]])
numpy.linalg.inv(m)
array([[ 0., 1., -1.],
[ 1., 0., 0.],
[-1., 0., 1.]])
Snadno si můžeme otestovat, že po vynásobení původní matice a matice inverzní dostaneme jednotkovou matici:
m2=numpy.linalg.inv(m)
numpy.dot(m,m2)
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
Při výpočtu se samozřejmě provádí kontroly, zda je možné inverzní matici vypočítat, tj. zda není původní matice singulární:
In [6]: m5
Out[6]:
array([[100, 101, 102, 103, 104],
[105, 106, 107, 108, 109],
[110, 111, 112, 113, 114],
[115, 116, 117, 118, 119],
[120, 121, 122, 123, 124]])
m5inv=numpy.linalg.inv(m5)
---------------------------------------------------------------------------
LinAlgError Traceback (most recent call last)
<ipython-input-7-aacc01ed4fc8> in <module>()
----> 1 m5inv=numpy.linalg.inv(m5)
/usr/lib/python3/dist-packages/numpy/linalg/linalg.py in inv(a)
518 signature = 'D->D' if isComplexType(t) else 'd->d'
519 extobj = get_linalg_error_extobj(_raise_linalgerror_singular)
--> 520 ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
521 return wrap(ainv.astype(result_t))
522
/usr/lib/python3/dist-packages/numpy/linalg/linalg.py in _raise_linalgerror_singular(err, flag)
88
89 def _raise_linalgerror_singular(err, flag):
---> 90 raise LinAlgError("Singular matrix")
91
92 def _raise_linalgerror_nonposdef(err, flag):
LinAlgError: Singular matrix
10. Vyřešení systému lineárních rovnic
Další užitečnou funkcí (asi nejvíce pro studenty 🙂 je funkce nazvaná numpy.linalg.solve, která slouží pro vyřešení systému lineárních rovnic. Tato funkce akceptuje dva parametry – matici s koeficienty původních rovnic a vektor obsahující pravé strany původních rovnic. Nejprve se podívejme na triviální příklad jediné rovnice:
2x = 10
Matice s koeficienty obsahuje jediný prvek – dvojku. Vektor pravých stran obsahuje taktéž jediný prvek – 10. Řešení tedy získáme takto:
a=numpy.array([[2]]) b=numpy.array([10]) numpy.linalg.solve(a,b) array([ 5.])
Důkaz, že je řešení x=5 správné, asi není zapotřebí provádět...
V případě soustavy dvou rovnic:
x + y = 2 x - y = 0
budeme postupovat následovně:
# matice koeficientů původních rovnic # [1,1] znamená 1*x + 1*y a=numpy.array([ [1,1] , [1,-1] ]) # matice pravých stran rovnic b=numpy.array([2,0]) # výpočet numpy.linalg.solve(a,b) array([ 1., 1.])
Dostali jsme podle očekávání výsledek x=1 a y=1.
Zadání posledního příkladu jsem získal z adresy http://www.matematika.cz/systemy-linearnich-rovnic:
2x1 + 3x2 + 7x3 = 47
3x1 + 8x2 + x3 = 50
3x2 + 3x3 = 27
Proveďme výpočet této soustavy:
a=numpy.array([[2,3,7],[3,8,1],[0,3,3]]) b=numpy.array([47,50,27]) numpy.linalg.solve(a,b) array([ 2., 5., 4.])
Výsledek tedy je: x1=2, x2=5 a x3=4, což je ostatně možné si ověřit na výše uvedené adrese.
11. Předchozí části seriálu
- Vývojová prostředí ve Fedoře (1. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-1-dil/ - Vývojová prostředí ve Fedoře (2. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-2-dil/ - Vývojová prostředí ve Fedoře (3. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-3-dil/ - Vývojová prostředí ve Fedoře (4. díl)
http://mojefedora.cz/vyvojova-prostredi-ve-fedore-4-dil/ - Integrovaná vývojová prostředí ve Fedoře: PyDev
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Integrovaná vývojová prostředí ve Fedoře: PyDev (2.část)
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev-2-cast/ - Integrovaná vývojová prostředí ve Fedoře: IPython a IPython Notebook
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-ipython-a-ipython-notebook/ - Integrovaná vývojová prostředí ve Fedoře: praktické použití IPython Notebooku a knihovny Numpy
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-prakticke-pouziti-ipython-notebooku-a-knihovny-numpy/
12. Odkazy na Internetu
- Systémy lineárních rovnic
http://www.matematika.cz/systemy-linearnich-rovnic - IPython homepage
http://ipython.org/ - Dokumentace k IPythonu
http://ipython.org/documentation.html# - IPython Tutorial
http://ipython.readthedocs.org/en/stable/interactive/tutorial.html - NumPy Home Page
http://www.numpy.org/ - NumPy v1.10 Manual
http://docs.scipy.org/doc/numpy/index.html - NumPy (Wikipedia)
https://en.wikipedia.org/wiki/NumPy - Matplotlib Home Page
http://matplotlib.org/ - matplotlib (Wikipedia)
https://en.wikipedia.org/wiki/Matplotlib - The cell magics in IPython
http://nbviewer.jupyter.org/github/ipython/ipython/blob/1.x/examples/notebooks/Cell%20Magics.ipynb - 0MQ Home Page
http://zeromq.org/ - Is IPython Notebook ever used as an IDE, or merely for presentations?
https://www.reddit.com/r/IPython/comments/1uk7hp/is_ipython_notebook_ever_used_as_an_ide_or_merely/ - The IDE as a Bad Programming Language Enabler
https://dzone.com/articles/ide-bad-programming-language - Enhanced Interactive Python with IPython
http://www.onlamp.com/pub/a/python/2005/01/27/ipython.html - Direct mode
https://en.wikipedia.org/wiki/Direct_mode - Seznámení s Python IDE Spyder (článek vyšel zde na mojefedora.cz)
http://mojefedora.cz/seznameni-s-python-ide-spyder/ - Stránka s popisem různých IDE pro Python
http://quintagroup.com/cms/python/ide - Eclipse (stránka o frameworku na Fedoraproject.org)
https://fedoraproject.org/wiki/Eclipse - PyDev (hlavní stránka)
http://pydev.sourceforge.net/index.html - PyDev (download, v podstatě není zapotřebí)
http://pydev.sourceforge.net/download.html - PyDev (stránka s metainformacemi o PyDev pluginu, použita v Eclipse)
http://www.pydev.org/updates/ - PyDev (stránka s pluginem, použita v Eclipse)
https://dl.bintray.com/fabioz/pydev/4.5.4/ - Certifikát, který lze do Eclipse doinstalovat
http://www.pydev.org/pydev_certificate.cer - PyDev FAQ
http://pydev.sourceforge.net/faq.html - PyDev (Wikipedia)
https://en.wikipedia.org/wiki/PyDev - Python (oficiální stránky projektu)
https://www.python.org/ - Jython
http://www.jython.org/ - IronPython
http://ironpython.net/ - Python 3.5.1 documentation
https://docs.python.org/3/ - PyDev: Unittest integration
http://mojefedora.cz/integrovana-vyvojova-prostredi-ve-fedore-pydev/ - Continuous unit testing with Pydev (Python and Eclipse)
http://stackoverflow.com/questions/1015581/continuous-unit-testing-with-pydev-python-and-eclipse - Test-driven development
https://en.wikipedia.org/wiki/Test-driven_development


